Question

The angles of depression of the top and bottom of a building 50 meters high as 4 observed from the top of a tower are 30 and 60, respectively. Find the height of the tower and also the horizontal distance between the building and the tower.

Answer 1

Hint: Draw figure with the given statement considering the triangle formed. By using basic trigonometric functions, take the tangent value of both triangles i.e. $\tan {{30}^{\circ }}$ and $\tan {{60}^{\circ }}$. Thus, find the height and the distance.

Complete step-by-step answer:

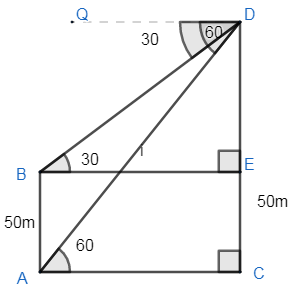
Consider the figure that has been drawn. Let AB be the building of 50m. CD is the tower. Now from point A top of the tower is at angle ${{60}^{\circ }}$.From point B the top of the tower is at angle ${{30}^{\circ }}$ .Let the distance between the building and tower be AC. The angle of depression to the top of the building $=\angle QDB={{30}^{\circ }}$ .
Similarly the angle of depression to the bottom of building $=\angle QDA={{60}^{\circ }}$ .
Now, let from the figure we can say that BE is parallel to AC and QD. Which means that $BE\parallel AB$ and $BE\parallel QD$ .
Thus $AB=CE=50m$ (from figure).
Lines DQ and BE are parallel, thus BD is the transversal. So, $\angle DBE=\angle QDB={{30}^{\circ }}$ , i.e. they are alternate angles.
Similarly AB and CE are parallel lines. So, AC=BE. $AB\parallel QD$ , So, AD is the transversal.
So, $\angle QDA=\angle DAC={{60}^{\circ }}$ .
First let we consider $\Delta DBE$ , which is a right $\Delta le$ as DC. Is perpendicular to AC, i.e. $DC\bot AC$ .
$\therefore $ from $\Delta DBE$
$\tan {{30}^{\circ }}=\dfrac{\text{opposite side}}{\text{hypotenuse}}=\dfrac{DE}{AD}$ .
We know from the trigonometric table that $\tan {{30}^{\circ }}=\dfrac{1}{\sqrt{3}}$
$\begin{align}
  & \therefore \dfrac{1}{\sqrt{3}}=\dfrac{DE}{BE} \\
 & \therefore BE=\sqrt{3}DE \\
\end{align}$
Now consider $\Delta DAC$
$\tan {{60}^{\circ }}=\dfrac{\text{opposite side}}{\text{hypotenuse}}=\dfrac{DC}{AC}$
From the trigonometric table we know that $\tan {{60}^{\circ }}=\sqrt{3}$ .
$\therefore \sqrt{3}=\dfrac{DE+EC}{AC}=\dfrac{DE+50}{AC}$ .
We said that $AC=BE$ .
$\therefore \sqrt{3}=\dfrac{DE+50}{BE}$ , now put $BE=\sqrt{3}DE$ in the expression
$\therefore \sqrt{3}=\dfrac{DE+50}{\sqrt{3}DE}$ , Apply cross multiplication properly.
$\sqrt{3}\times \sqrt{3}DE=DE+50$
$\begin{align}
  & \therefore 3DE=DE+50\Rightarrow 3DE-DE=50 \\
 & \therefore 2DE=50,\text{ So }DE=\dfrac{50}{2}=25 \\
\end{align}$
Thus we got $DE=25m$ .
The total height of the tower$=DE+EC=DC=75m$ .
Now, let us fix the distance between the building and town.
$AC=BE=\sqrt{3}DE$ put $DE=25m$
$\therefore AC=25\sqrt{3}m$
Thus, the distance between building and tower $=25\sqrt{3}m$ .
Hence we got the height of the tower as 75m and the distance between them is $25\sqrt{3}$ m

Note: We have been given the angle of depression which is the angle from the top of the light house to the top and bottom of the building. But as the lines formed are parallel they become alternate angles. So, the elevation from top and bottom become ${{30}^{\circ }}$ and ${{60}^{\circ }}$ .