Question

The angles between the lines $x\cos \alpha +y\sin \alpha =a$ and $x\sin \beta -y\cos \beta =a$ is
(a) $\beta -\alpha $
(b) $\pi +\beta -\alpha $
(c) $\dfrac{\pi }{2}+\beta +\alpha $
(d) $\dfrac{\pi }{2}-\beta +\alpha $

Answer 1

Hint:The formula to find angle between two lines is given by $\tan \theta =\left| \left. \dfrac{{{m}_{2}}-{{m}_{1}}}{1+{{m}_{1}}{{m}_{2}}} \right| \right.$ and after using ${{\tan }^{-1}}$ on both the sides of the equation will imply ${{\tan }^{-1}}\left( \tan \theta \right)={{\tan }^{-1}}\left| \left. \dfrac{{{m}_{2}}-{{m}_{1}}}{1+{{m}_{1}}{{m}_{2}}} \right| \right.$. Thus the direct formula is given by $\theta ={{\tan }^{-1}}\left| \left. \dfrac{{{m}_{2}}-{{m}_{1}}}{1+{{m}_{1}}{{m}_{2}}} \right| \right.$. Here ${{m}_{1}}$ and ${{m}_{2}}$ are slopes of their respected lines.

Complete step-by-step answer:
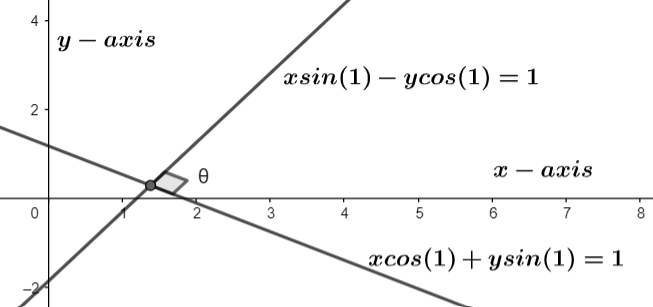
The figure for equations $x\cos \alpha +y\sin \alpha =a\,,\,x\sin \beta -y\cos \beta =a$ by considering its particular equation a=1 is shown below

Now we consider general equation for a straight line $y=mx+c$
Consider the given equation $x\cos \alpha +y\sin \alpha =a$ and solve it by leaving y on the left side of the equal sign and the rest on the right side of the equal sign. Therefore we get,
$\begin{align}
  & y\sin \alpha =a-x\cos \alpha \\
 & y=\dfrac{-\cos \alpha }{\sin \alpha }x+\dfrac{a}{\sin \alpha } \\
\end{align}$
Comparing $y=\dfrac{-\cos \alpha }{\sin \alpha }x+\dfrac{a}{\sin \alpha }$ with the general equation $y={{m}_{1}}x+c$ we get the slope ${{m}_{1}}=\dfrac{-\cos \alpha }{\sin \alpha }$ here $\dfrac{-\cos \alpha }{\sin \alpha }$ can be written as $-\cot \alpha $ and the other expression for $-\cot \alpha $ is given by $-\dfrac{1}{\tan \alpha }$
Now we find the slope for equation $x\sin \beta -y\cos \beta =a$ by taking required terms to the right side of the expression resulting into $y\cos \beta =\dfrac{a}{\cos \beta }+x\dfrac{\sin \beta }{\cos \beta }$ and dividing whole equation by $\cos \beta $ we get $y=x\dfrac{\sin \beta }{\cos \beta }-\dfrac{a}{\cos \beta }$
Now comparing $y=+\dfrac{\sin \beta }{\cos \beta }x-\dfrac{a}{\cos \beta }$ with standard equation of line $y={{m}_{2}}x+c$ we get
${{m}_{2}}=+\dfrac{\sin \beta }{\cos \beta }$ also $\dfrac{\sin \beta }{\cos \beta }$ can be written as $\tan \beta $
Clearly the slopes are not parallel since ${{m}_{1}}\ne {{m}_{2}}$
Now to find the angle between the lines we use the formula $\tan \theta =\left| \left. \dfrac{{{m}_{1}}-{{m}_{2}}}{1+{{m}_{1}}{{m}_{2}}} \right| \right.$
$\begin{align}
  & \Rightarrow \tan \theta =\left| \left. \dfrac{\left( \dfrac{-\cos \alpha }{\sin \alpha } \right)-\left( \dfrac{\sin \beta }{\cos \beta } \right)}{1+\left( \dfrac{-\cos \alpha }{\sin \alpha } \right)\left( \dfrac{\sin \beta }{\cos \beta } \right)} \right| \right. \\
 & \Rightarrow \tan \theta =\left| \left. \dfrac{\left( \dfrac{-\cos \alpha }{\sin \alpha } \right)-\dfrac{\sin \beta }{\cos \beta }}{1+\left( \dfrac{-\cos \alpha }{\sin \alpha } \right)\left( \dfrac{\sin \beta }{\cos \beta } \right)} \right| \right. \\
\end{align}$
Therefore we get,
$\tan \theta =\left| \left. \dfrac{\left( \dfrac{-\cos \alpha \cos \beta -\sin \beta \sin \alpha }{\sin \alpha \cos \beta } \right)}{\dfrac{\sin \alpha \cos \beta -\cos \alpha \sin \beta }{\sin \alpha \cos \beta }} \right| \right.$
Apply simplification here by cancelling the common term $\sin \alpha \cos \beta $ in numerator and denominator. After this we will be left with $\left| \left. \dfrac{-\cos \alpha \cos \beta -\sin \beta \sin \alpha }{\sin \alpha \cos \beta -\cos \alpha \sin \beta } \right| \right.$
Now open the modulus and it will result into a positive expression $\left| \left. \dfrac{-\cos \alpha \cos \beta -\sin \beta \sin \alpha }{\sin \alpha \cos \beta -\cos \alpha \sin \beta } \right| \right.=\dfrac{\cos \alpha \cos \beta +\sin \beta \sin \alpha }{\sin \alpha \cos \beta -\cos \alpha \sin \beta }....(ii)$
Now we use the following formulas $\cos \left( A-B \right)=\cos A\cos B-\sin A\sin B\,,\,\sin \left( A-B \right)=\sin A\cos B-\cos A\sin B$ in equation $(ii)$ we get,
$\begin{align}
  & \dfrac{\cos \alpha \cos \beta +\sin \beta \sin \alpha }{\sin \alpha \cos \beta -\cos \alpha \sin \beta }=\dfrac{\cos \left( \alpha -\beta \right)}{\sin \left( \alpha -\beta \right)} \\
 & \Rightarrow \dfrac{\cos \alpha \cos \beta +\sin \beta \sin \alpha }{\sin \alpha \cos \beta -\cos \alpha \sin \beta }=\cot \left( \alpha -\beta \right) \\
 & \Rightarrow \tan \theta =\cot \left( \alpha -\beta \right) \\
\end{align}$
The term $\cot \left( \alpha -\beta \right)$ can also be written as $\tan \left( \dfrac{\pi }{2}+\left( \alpha -\beta \right) \right)$
Therefore we get $\tan \left( \dfrac{\pi }{2}+\left( \alpha -\beta \right) \right)=\tan \left( \dfrac{\pi }{2}+\alpha -\beta \right)$
This gives the value of $\tan \theta =\tan \left( \dfrac{\pi }{2}+\alpha -\beta \right)$ and after using ${{\tan }^{-1}}$ on both the sides of the equation will imply ${{\tan }^{-1}}\left( \tan \left( \dfrac{\pi }{2}+\left( \alpha -\beta \right) \right) \right)={{\tan }^{-1}}\left( \tan \left( \dfrac{\pi }{2}+\alpha -\beta \right) \right)$
Hence the correct option is (d).

Note: By focusing on trigonometric terms and finding slopes implies option (d). Otherwise if any mistake is done between angles and their signs will imply either option (a) or (c). It is clear that the lines are not parallel since the slopes are not equal. But here it cannot be said that the angle can be 90 degrees. So in one go apply the formula for finding angle between two lines directly. This will imply the answer faster.
We could have solved it by the formula for slope. But here no points are given directly. That is why the method of comparing equations with the standard equation of line is used here.

In the figure below we can see that the slope of the line is $\theta $

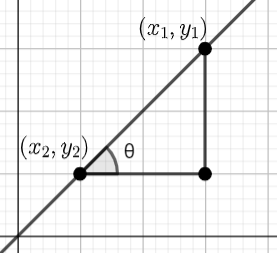
Taking figure as a guide the formula of the slope is given by $m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$