Question

The angle of the prism is \[{{30}^{0}}\]. The rays incident at \[{{60}^{0}}\]at one refracting face suffers a deviation of \[{{30}^{0}}\]. Then, the angle of emergence is:
 $\begin{align}
  & A.\quad {{0}^{0}} \\
 & B.\quad {{30}^{0}} \\
 & C.\quad {{60}^{0}} \\
 & D.\quad {{90}^{0}} \\
\end{align} $

Answer 1

Hint: To solve this problem, one must know the prism relation in between the angle of incidence (i), angle of emergence (e), the angle of the prism (A) and the angle of deviation $\left( \delta \right) $, given by: $\delta +A=i+e $. Substituting in the given values from the problem into this equation will give us the solution.

Complete step-by-step answer:
Let’s start by understanding what a prism is. In physics, a prism is a glass or any other transparent object, which is in the shape of a solid triangle with the refracting surfaces at an acute angle to each other.
When a beam of monochromatic light is incident on one of the refracting surfaces of the prism, the beam undergoes refraction twice upon emerging out of the prism. The first refraction occurs at the interface between the air and the glass of the prism and the second refraction occurs at the other refracting surface, where the light beam is passing through the glass to air.
Below, is a diagram depicting the refraction occurring.

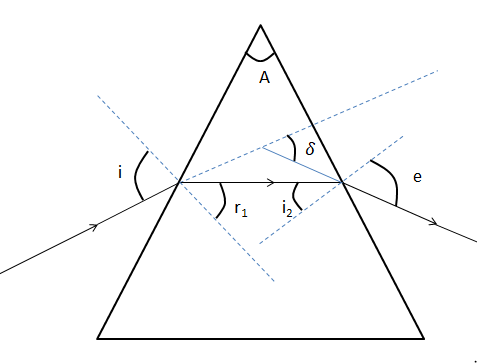
Here, angle (A) refers to the angle of the prism. The angle (i) is the angle of incidence of the light beam on the prism. The angle (e) refers to the final angle of emergence of the light beam with respect to the prism and the angle $\left( \delta \right) $ is the net angle of deviation of the beam from the originally incident path. The angle $\left( {{r}_{2}} \right) $ is the angle of refraction of the incident beam and the angle $\left( {{i}_{1}} \right) $ is the angle of the first refracted ray being incident on the glass-air interface for second refraction.
Hence, for a monochromatic light beam, the relation is: $\delta +A=i+e $.
In the problem, we are given the angle of prism $\left( A={{30}^{0}} \right) $and the angle of deviation of the light beam as $\left( \delta ={{30}^{0}} \right) $. The light beam was incident at $\left( i={{60}^{0}} \right) $. Putting in these values, we get: $\delta +A=i+e\Rightarrow {{30}^{0}}+{{30}^{0}}={{60}^{0}}+e\Rightarrow {{60}^{0}}={{60}^{0}}+e\Rightarrow e={{0}^{0}} $.
Hence, the angle of emergence is $e={{0}^{0}} $, given by Option A.

Note: We must remember, that the above formula of ( $\delta +A=i+e $) is only valid for a monochromatic light, since the angle of deviation will be different for different values of frequencies of the light.
An example of this is the dispersion of white light into its constituent VIBGYOR colors upon passing through the prism. This occurs because the Violet light has a larger angle of deviation as compared to the Red light, since the violet and red lights have different frequencies.