Question

The angle of elevation of the top of a tower from two points of distances a and b meters from the base and in the same straight line with it are $\alpha $and $\beta $ respectively, prove that the height of the tower is $h = \dfrac{{(a - b)\tan \alpha \tan \beta }}{{\tan \beta - \tan \alpha }}$

Answer 1

Hint: First we will represent the question in a diagram format and then find out the various relations and then prove the height of the tower. While solving we will get 2 relations in $\alpha$ and $\beta$. We equate those two equations and we get the value of h.

Complete step-by-step answer:
In the question stated as the given as, the height of the tower is $h$,
Also, the distances from the tower are $a$ and $b$, the elevation from distance $a$ is $\alpha $ and the elevation from distance $b$ is $\beta $.
The diagram for the problem could be made as:

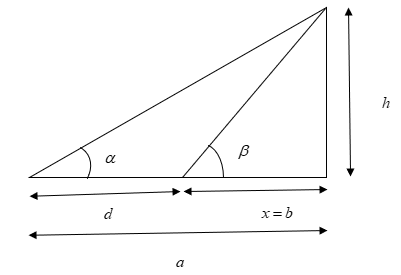
From the above diagram we see that $d = a - b \to (1)$
Also, we consider $b$ being $x$.
Now, we use the formula for $\tan \theta = \dfrac{{adjacent}}{{base}}$
From the diagram we can write it as, $\tan \alpha = \dfrac{h}{{d + x}}$ and $\tan \beta = \dfrac{h}{x}$
Here we have to consider, $\tan \beta = \dfrac{h}{x}$
On cross multiplying we get:
$ \Rightarrow x = \dfrac{h}{{\tan \beta }}$
Now let’s consider $\tan \alpha = \dfrac{h}{{d + x}} \to \left( 2 \right)$
On substituting value of $x$ in equation $\left( 2 \right)$ we get:
$ \Rightarrow \tan \alpha = \dfrac{h}{{d + \dfrac{h}{{\tan \beta }}}}$
On cross multiplying we get,
$ \Rightarrow \tan \alpha \times \left( {d + \dfrac{h}{{\tan \beta }}} \right) = h$
On simplifying we get:
$ \Rightarrow d \times \tan \alpha + h \times \dfrac{{\tan \alpha }}{{\tan \beta }} = h$
On transferring $h \times \dfrac{{\tan \alpha }}{{\tan \beta }}$ across the $ = $ sign we get:
\[ \Rightarrow d \times \tan \alpha = h - h \times \dfrac{{\tan \alpha }}{{\tan \beta }}\]
On taking $h$ common in the right-hand side we get:
\[ \Rightarrow d \times \tan \alpha = h\left( {1 - \dfrac{{\tan \alpha }}{{\tan \beta }}} \right)\]
Therefore, the equation can be re-written as:
\[ \Rightarrow \dfrac{{d \times \tan \alpha }}{{1 - \dfrac{{\tan \alpha }}{{\tan \beta }}}} = h\]
On taking LCM we get,
\[ \Rightarrow \dfrac{{d \times \tan \alpha }}{{\dfrac{{\tan \beta - \tan \alpha }}{{\tan \beta }}}} = h\]
On taking reciprocal we get,
$ \Rightarrow h = \dfrac{{d \times \tan \beta \tan \alpha }}{{\tan \beta - \tan \alpha }}$
Now from equation $(1)$ we know $d = a - b$ therefore on substituting the value we get:
$ \Rightarrow h = \dfrac{{(a - b) \times \tan \alpha \tan \beta }}{{\tan \beta - \tan \alpha }}$

Therefore, the height of the tower can be represented by, $h = \dfrac{{(a - b) \times \tan \alpha \tan \beta }}{{\tan \beta - \tan \alpha }}$

Note: The trigonometric relations between the various sides of a right triangle and the sides should be known.
It is to be noted that ${{sin \theta = }}\dfrac{{{\text{opposite side}}}}{{{\text{hypotenuse}}}}$ and ${{cos \theta = }}\dfrac{{{\text{adjacent side}}}}{{{\text{hypotenuse}}}}$
${{tan \theta = }}\dfrac{{{\text{opposite side}}}}{{{\text{adjacent side}}}}$