Question

The angle of elevation of an airplane from a point on the ground is \[{{60}^{0}}\]. After a flight of 30 seconds, the angle of elevation becomes \[{{30}^{0}}\]. If the airplane is flying at a constant height of \[3000\sqrt{3}\text{ m}\], find the speed of the airplane.

Answer 1

Hint: To solve this problem, we have to illustrate the situation first. Draw the diagram of the given situation. Then after that we should use all possible sin, cos, tan formulas to solve the problem. We know that in a \[\Delta \text{ABC}\], \[\sin A=\dfrac{\text{Opposite side to angle A}}{\text{Hypotenuse of }\Delta \text{ABC}}\], \[\operatorname{cosA}=\dfrac{\text{Adjacent side to angle A}}{\text{Hypotenuse of }\Delta \text{ABC}}\] and \[sinA=\dfrac{\text{Opposite side to angle A}}{\text{Adjacent side to angle A}}\]. By these formulae, we should find the distance travelled by airplane during the flight of 30 s. We know that \[velocity=\dfrac{\text{speed}}{\text{time}}\]. By using this formula, we can find the velocity of an airplane.

Complete step-by-step solution -
Let us assume a line AB. Let us take point A on the ground as a reference point. Consider an airplane flying at a constant height of \[3000\sqrt{3}\text{ m}\]. Initially the airplane is at point C which makes an angle \[{{60}^{0}}\] with respective to point A. Let us draw a perpendicular from point C to point E on line AB. After a flight of 30s, the airplane reaches point D. At point D, the flight makes an angle \[{{30}^{0}}\] with respective to point A. Let us draw a perpendicular from point D to point F on the line AB. This situation is illustrated in the below diagram.

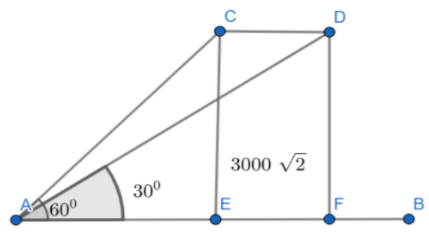
From the diagram,
\[\begin{align}
  & CE=DF=3000\sqrt{3}\text{ m}.....\text{(1)} \\
 & \angle CAB={{60}^{0}}.......(2) \\
 & \angle DAB={{30}^{0}}.......(3) \\
\end{align}\]
In \[\Delta ACE\],
\[tan\angle CAB=\dfrac{CE}{AE}\]
From equation (1) and equation (2),
\[\begin{align}
  & tan{{60}^{0}}=\dfrac{3000\sqrt{3}}{AE} \\
 & \Rightarrow \sqrt{3}=\dfrac{3000\sqrt{3}}{AE} \\
\end{align}\]
By cross multiplication,
\[\begin{align}
  & \Rightarrow AE\sqrt{3}=3000\sqrt{3} \\
 & \Rightarrow AE=3000.....(4) \\
\end{align}\]
In \[\Delta ADF\],
\[Tan\angle DAB=\dfrac{DF}{AF}\]
From equation (2),
\[\begin{align}
  & tan{{30}^{0}}=\dfrac{DF}{AF} \\
 & \Rightarrow \dfrac{1}{\sqrt{3}}=\dfrac{3000\sqrt{3}}{AF} \\
\end{align}\]
By cross multiplication,
\[\begin{align}
  & \Rightarrow 3000\sqrt{3}(\sqrt{3})=2AF \\
 & \Rightarrow AF=9000.....(5) \\
\end{align}\]
From equation (4) and equation (5),
\[\begin{align}
  & \Rightarrow 9000=3000+EF \\
 & \Rightarrow EF=6000.....(6) \\
\end{align}\]
The time required for an airplane to travel from point C and point D.
From the diagram, it is clear that CD is equal to EF.
From equation (6),
\[CD=6000m\]
\[\text{Speed of airplane = }\dfrac{CD}{{{t}_{CD}}}\]
where \[{{t}_{CD}}\] is the time required by flight to travel from point C to point D.
\[\text{Speed of airplane = }\dfrac{6000m}{30s}=200m/s\].
Therefore, the speed of an airplane is equal to \[200m/s.\].

Note: The diagram should be drawn correctly while solving this question. We should assume the airplane follows a straight path but not a curved path. Because in the question it is clearly mentioned that the airplane follows a straight path. If we assume a curved path, it will give a different answer. We needed to find the distance travelled by airplane during the flight of 30 s. We should only take CD for calculating the speed of the airplane. We should not take AF (or) CF for calculating the speed of an airplane.