Question

The angle of elevation of a chord from a point ‘h’ m above the lake is\[\alpha \]and angle of depression of reflection in the lake is\[\beta \]. Prove that the height of the cloud from surface of water is
\[\dfrac{h\left( \tan \beta +\tan \alpha \right)}{\tan \beta -\tan \alpha }\].

Answer 1

Hint: Draw the figure as per mentioned in the question. The angle of elevation of cloud is at a height h and above the lake. Take the height of the cloud from the lake as x. The height of elevation and depression of reflection of clouds is the same. Consider the triangles formed and solve it to get an expression for x.

Complete step-by-step answer:

Let us assume that p is the point which is at ‘h’ meters distance from the lake is taken as C’. Refer to the figure.

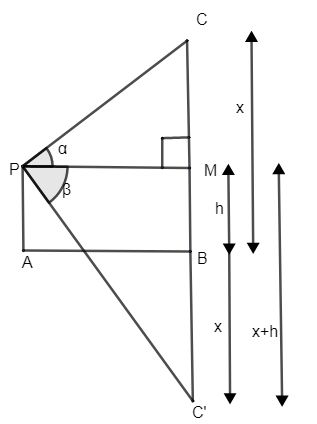
Let us assume that the distance of the cloud from the lake is ‘x’ meters.
\[\therefore \]\[\alpha \]represents the angle of elevation of cloud above the lake and\[\beta \]represents the angle of depression of reflection of cloud in the lake.
We can say that,
\[BC=B{{C}^{'}}=x\].
From the figure we can make out that AP = BM = h.
\[\therefore \]The length is
\[{{C}^{'}}M=B{{C}^{'}}+MB=x+h\].
Let us consider,\[\vartriangle CPM\] where\[\angle CPM=\alpha \] and right angled at M, so\[\vartriangle CPM\] is a right angle triangle. By basic trigonometry,
\[\tan \alpha \]= opposite side/ adjacent side =\[\dfrac{CM}{PM}\].
\[\Rightarrow \tan \alpha =\dfrac{CM}{PM}\Rightarrow PM=\dfrac{CM}{\tan \alpha }=\dfrac{x-h}{\tan \alpha }\]
\[CB=CM+MB\]
\[CM=x-h\]
\[\therefore PM=\dfrac{x-h}{\tan \alpha }-(1)\]
Now consider,\[\vartriangle PM{{C}^{'}}\]
\[\tan \beta =\dfrac{C{{M}^{'}}}{PM}\]
\[\Rightarrow PM=\dfrac{x+h}{\tan \beta }-(2)\][From figure]
Equate both equation (1) and (2) and cross multiplying.
\[\dfrac{x+h}{\tan \alpha }=\dfrac{x+h}{\tan \beta }\]
\[\tan \beta \left( x-h \right)=\left( x+h \right)\tan \alpha \]
\[\Rightarrow x\tan \beta -h\tan \beta =x\tan \alpha +h\tan \alpha \]
\[h\left( \tan \alpha +\tan \beta \right)=x\left( \tan \beta -\tan \alpha \right)\]
\[\therefore x=\dfrac{h\left( \tan \alpha +\tan \beta \right)}{\tan \beta -\tan \alpha }\]
Hence proved.

Note: Remember to take the value of the height of the cloud from the lake i.e. elevation of cloud and depression of reflection of cloud as x. So it makes\[BC=B{{C}^{'}}=x\]. Solution of the two triangles formed from the surface of the lake to the elevation and reflection will give us the value of ‘x’.