Question

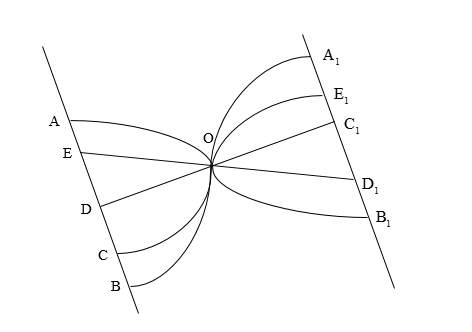
The adjoining figure shows the road plan of lines connecting two parallel roads AB and \[{{\rm{A}}_1}{{\rm{B}}_1}\]. A man walking on the road AB takes a turn at random to reach the road \[{{\rm{A}}_1}{{\rm{B}}_1}\]. It is known that he reaches the road \[{{\rm{A}}_1}{{\rm{B}}_1}\] from O by taking a straight line path. The chance that he moves on a straight line from the road AB to \[{{\rm{A}}_1}{{\rm{B}}_1}\] is
(a) \[0.25\]
(b) \[0.04\]
(c) \[0.2\]
(d) None of these

Answer 1

Hint:
Here, we will assume \[X\] to be the event that the man takes any of the 5 paths from AB to O, and then takes one of the two straight paths from O to \[{{\rm{A}}_1}{{\rm{B}}_1}\]. Again we will assume \[Y\] to be the event that the man takes any one of the 2 straight paths from AB to \[{{\rm{A}}_1}{{\rm{B}}_1}\]. We will use the formula for conditional probability to find the probability \[P\left( {Y|X} \right)\], and hence, find the required chance.

Complete step by step solution:
We can observe that from AB to O, the two straight paths are from point E, and point D.
We can also observe that form O to \[{{\rm{A}}_1}{{\rm{B}}_1}\], the two straight paths are from O to \[{{\rm{C}}_1}\], or \[{{\rm{D}}_1}\].
We will use conditional probability to find the required chance.
Let \[X\] be the event that the man takes any of the 5 paths from AB to O, and then takes one of the two straight paths from O to \[{{\rm{A}}_1}{{\rm{B}}_1}\].
The number of ways in which the man takes any one path of the 5 paths from AB to O is given by \[{}^5{C_1} = 5\] ways.
The number of ways in which the man takes any one path of the 2 straight paths from O to \[{{\rm{A}}_1}{{\rm{B}}_1}\] is given by \[{}^2{C_1} = 2\] ways.
Therefore, we get
The number of ways in which the man takes any one path of the 5 paths from AB to O, and then takes any one path of the 2 straight paths from O to \[{{\rm{A}}_1}{{\rm{B}}_1}\] is given by \[5 \times 2 = 10\] ways.
Thus, we get
\[P\left( X \right) = 10\]
The straight paths from AB to \[{{\rm{A}}_1}{{\rm{B}}_1}\] are the paths \[{\rm{D}}{{\rm{C}}_1}\] and \[{\rm{E}}{{\rm{D}}_1}\].
Let \[Y\] be the event that the man takes any one of the 2 straight paths from AB to \[{{\rm{A}}_1}{{\rm{B}}_1}\].
The number of ways in which the man takes any one path of the 2 straight paths from AB to \[{{\rm{A}}_1}{{\rm{B}}_1}\] is given by \[{}^2{C_1} = 2\] ways.
Therefore, we get
\[P\left( Y \right) = 2\]
Now, we need to find the intersection of the events \[X\] and \[Y\].
The event \[X\] is the event that the man takes any of the 5 paths from AB to O, and then takes one of the two straight paths from O to \[{{\rm{A}}_1}{{\rm{B}}_1}\].
The event \[Y\] is the event that the man takes any one of the 2 straight paths from AB to \[{{\rm{A}}_1}{{\rm{B}}_1}\].
Therefore, the intersection of the events \[X\] and \[Y\] is the event that the man takes one of the two straight paths from AB to \[{{\rm{A}}_1}{{\rm{B}}_1}\].
The number of ways in which the man takes any one path of the 2 straight paths from AB to \[{{\rm{A}}_1}{{\rm{B}}_1}\] is given by \[{}^2{C_1} = 2\] ways.
Therefore, we get
\[P\left( {X \cap Y} \right) = 2\]
Using the formula for conditional probability, we get
\[ \Rightarrow P\left( {Y|X} \right) = \dfrac{{P\left( {Y \cap X} \right)}}{{P\left( X \right)}}\]
Rewriting the expression, we get
\[ \Rightarrow P\left( {Y|X} \right) = \dfrac{{P\left( {X \cap Y} \right)}}{{P\left( X \right)}}\]
Substituting \[P\left( X \right) = 10\] and \[P\left( {X \cap Y} \right) = 2\] in the formula, we get
\[ \Rightarrow P\left( {Y|X} \right) = \dfrac{2}{{10}}\]
Therefore, we get
\[ \Rightarrow P\left( {Y|X} \right) = 0.2\]
Thus, given that the man reaches the road \[{{\rm{A}}_1}{{\rm{B}}_1}\] from O by taking a straight line path, the chance that he moves on a straight line from the road AB to \[{{\rm{A}}_1}{{\rm{B}}_1}\] is the chance is \[0.2\].

The correct option is option (c).


Note:
We used the formula for conditional probability to solve the problem. If it is given that an event \[B\] has happened, then the probability that \[A\] occurs after the happening of the event \[B\] is given by the conditional probability \[P\left( {A|B} \right) = \dfrac{{P\left( {A \cap B} \right)}}{{P\left( B \right)}}\].