
The acute angle that the vector
(a)
(b)
(c)
(d)
Answer
458.4k+ views
1 likes
Hint: First of all find a plane that is perpendicular to the two vectors given by taking the cross product using the determinant formula given as
Complete step by step solution:
Here we have been provided with a plane that contains two vectors
Let us assume the given two vectors that lie in a plane as
Expanding the determinant we get,
Now, let us assume that the acute angle between the plane containing
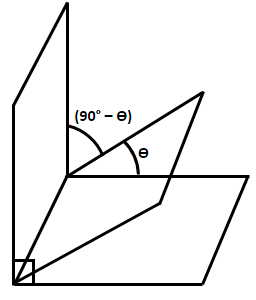
Considering the dot product of
We know that
We know that
We know that
Hence option (d) is the correct answer.
Note: We do not have any method to directly determine the equation of a plane containing two vectors and that is why we have found the perpendicular plane first. If we would have been provided with a point
Complete step by step solution:
Here we have been provided with a plane that contains two vectors
Let us assume the given two vectors that lie in a plane as
Expanding the determinant we get,
Now, let us assume that the acute angle between the plane containing

Considering the dot product of
We know that
We know that
We know that
Hence option (d) is the correct answer.
Note: We do not have any method to directly determine the equation of a plane containing two vectors and that is why we have found the perpendicular plane first. If we would have been provided with a point
Latest Vedantu courses for you
Grade 11 Science PCM | CBSE | SCHOOL | English
CBSE (2025-26)
School Full course for CBSE students
₹41,848 per year
Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Biology: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Trending doubts
Which one of the following is a true fish A Jellyfish class 12 biology CBSE

Which are the Top 10 Largest Countries of the World?

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Why is the cell called the structural and functional class 12 biology CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Derive an expression for electric potential at point class 12 physics CBSE




