Question

The 2 vectors $\hat j + \hat k$ and $3\hat i - \hat j + 4\hat k$ represent the two sides AB and AC, respectively of a $\Delta ABC$. The length of the median through A is
A. $\dfrac{{\sqrt {34} }}{2}$
B. $\dfrac{{\sqrt {48} }}{2}$
C. $\sqrt {18} $
D. None of these

Answer 1

Hint: Before attempting this question one should have prior knowledge about the vectors, sides of triangle and also remember that medium through A is given by $\overrightarrow {AD} = \dfrac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)$ here $\overrightarrow {AD} $ is the position vector of D and $\overrightarrow {AB} $ is the position vector of B and $\overrightarrow {AC} $ is the position vector of C, using this information we can approach the solution of the question.

Complete step by step answer:
According to the given information it is given that triangle ABC where $\overrightarrow {AB} = \widehat j + \hat k$ and $\overrightarrow {AC} = 3\widehat i - \hat j + 4\hat k$ are the sides.
Let D be the midpoint of BC such as AD is the median through A.
So, the resulting triangle is

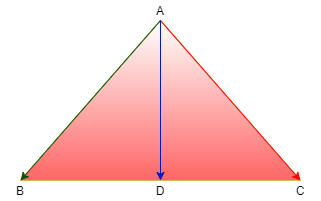
As we know, the length of any line is given by the magnitude of the vector which represents the line.
So, to find the length of the median through A is given by magnitude of that median and to find the magnitude of the median we have to find the position vector of D
We know that when D is the midpoint of BC
Then position vector of D = $\dfrac{1}{2}$(position vector of B + position vector of C) i.e. $\overrightarrow {AD} = \dfrac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)$
Therefore, $\overrightarrow {AD} = \dfrac{1}{2}\left( {\widehat j + \hat k + 3\widehat i - \hat j + 4\hat k} \right)$
$ \Rightarrow $$\overrightarrow {AD} = \dfrac{1}{2}\left( {3\widehat i + 5\hat k} \right)$
$\overrightarrow {AD} = \dfrac{3}{2}\widehat i + \dfrac{5}{2}\hat k$
So, we know that to find the length of median through A, we have to find the magnitude of AD
And the magnitude of any position vector $\overrightarrow {AB} $ (x, y, z) is given by $\left| {\overrightarrow {AB} } \right| = \sqrt {{x^2} + {y^2} + {z^2}} $
$AD = \sqrt {{{\left( {\dfrac{3}{2}} \right)}^2} + {{\left( 0 \right)}^2} + {{\left( {\dfrac{5}{2}} \right)}^2}} $
$ \Rightarrow $$AD = \sqrt {\dfrac{9}{4} + \dfrac{{25}}{4}} $
$ \Rightarrow $$AD = \sqrt {\dfrac{{34}}{4}} = \dfrac{{\sqrt {34} }}{2}$unit
Therefore, length of median through A is equal to $\dfrac{{\sqrt {34} }}{2}$

So, the correct answer is “Option A”.

Note: In the above solution, we came across the term “position vector” which can be explained as line having two ends which consists of 2 points where one end point is fixed and other point is dynamic or the moving point which describes the position to the relative point so as the point moves the length of position vectors changes or the direction of the position vector or both the direction and length of the position vector will change.