Question

How the television signals are propagated derive the formula for the area that a T.V. signal will cover.

Answer 1

Hint: We first explain the transmission of TV signal from transmitter to receiver. Then, we will derive the formula using a diagram showing the height of the transmitter and distance of transmission through the surface of the earth.

Complete step by step answer:
A T.V. signal is transmitted to a tall transmitting antenna through a wire. The transmitter produces electromagnetic radio waves and radiates these waves into the air. The radio waves get transmitted through air to long distances. A receiver antenna receives the radio waves and transforms them into electric signals. But these radio waves, transmitted to very long distances, will not be received by the receiver with enough strength due to the curved shape of the earth and the attenuation of the waves. The range is the maximum distance up to which a signal can be received with proper intensity by the receiver. We can now calculate the range.

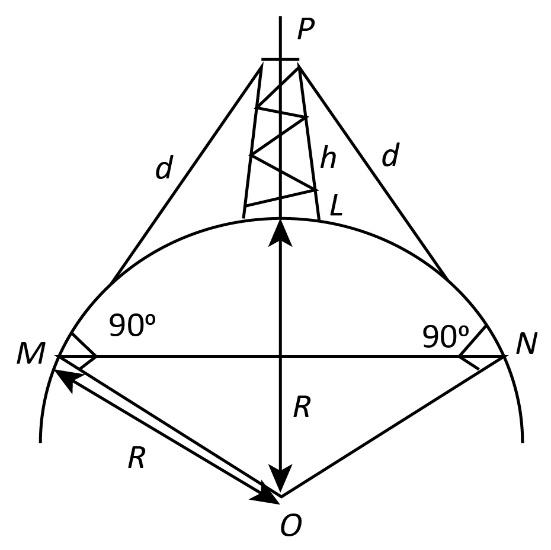
Let a transmitter of height $h$ be located at a point $L$ on the earth’s surface. $P$ is the top of the transmitter. The signal from point P can be transmitted with less attenuation till points $M$ and $N$ as shown in figure. Let $R$ be the radius of the earth and let $d$ be the range of transmission. From figure, we get

$d = PM = PN$

Also,
$
LP = h\\
OP = R
$

Hence, we can write
$
OP = OL + LP\\
 = R + h
$

Now we consider the triangle $POM$ in figure. Applying Pythagoras theorem to the triangle, we get

$
O{P^2} = P{M^2} + M{O^2}\\
\implies {\left( {R + h} \right)^2} = {d^2} + {R^2}\\
\implies {R^2} + {h^2} + 2Rh = {d^2} + {R^2}\\
\implies {d^2} = {h^2} + 2Rh
$

Since $R > > h$, we write
$
{d^2} = 2Rh\\
\implies d = \sqrt {2Rh}
$
Hence, $d = \sqrt {2Rh} $ is the range of the transmitting antenna.

Now, the area that can be covered by the T.V. signal can be written as
$A = \pi {d^2}\\
 = \pi \times 2Rh\\
 = 2\pi Rh
$.

So, the area that a T.V. The signal can cover $2\pi rh$ and it depends upon the height of the transmitter. It is why we see tall T.V. towers acting as transmitting antennas.

Note:
The signal from a small transmitting antenna is transmitted through wires to a tall transmitting antenna which is generally called T.V. tower. It is because of the high chance of attenuation of the signals from small transmitters. The tall transmitter enhances the signals it receives and then transmits it through long distances.