Question

Take four points P, Q, R, S in a plane. Draw lines by joining different pairs of points. How many lines can you draw in the following cases if three of these points are collinear?
A. $3$ lines
B. $4$ lines
C. $5$ lines
D. Data insufficient

Answer 1

Hint: In this geometrical problem, we are asked to take four points in a plane. Also we have given that the three points are collinear. With these conditions we need to find how many lines we can draw by joining different pairs of points. The important thing we need to keep in our mind is in the given four points three points are collinear.

Complete step-by-step solution:
Given four points in a plane are $P,Q,R,S$. In that three points are collinear.

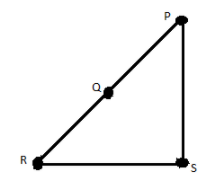
Therefore, we can draw $4$ lines by joining different pairs of points; they are $PQ,QR,RS,SP$.

Hence, the answer is option (B).

Additional Information: Three or more points are said to be collinear if they lie on a single straight line. A line on which points lie, especially if it is related to a geometric figure such as a triangle, is sometimes called an axis. Two points are trivially collinear since two points determine a line.

Note: Any three or more points are said to be collinear if there exists a line that passes through all three of these points. Any three or more lines are said to be concurrent if all three of these intersect at a common point. Here in this problem the points P, Q and R are collinear.