Question

Take any three non-collinear points A, B, C on a paper. How many lines in all can you draw through different pairs of the points? \[\]

Answer 1

Hint: We recall the definition of collinearity and non- collinearity of more than one point. We use the fact that we cannot draw more than one straight line passing through two points and try to find number of lines that can be draw using non-collinear points A, B, C. \[\]

Complete step by step answer:
We call more than points collinear if they lie on the same line and non-collinear if they do not lie on a straight line. We know that two points will always lie on some straight line and hence they are collinear. It also means that we can draw only one straight line passing through two points. \[\]
We are given the questions to take three points A, B, C on a paper and asked many lines in all can you draw through different pairs of the points. \[\]
We see that as the points A, B, C are non-collinear which means they do not lie in one straight line. We select A and B and draw line passing through which we can name as $\overleftrightarrow {AB}$ .We similarly join B and C to get the straight line $\overleftrightarrow{BC}$ and join A and C to get the straight line $\overleftrightarrow{AB}$. We draw the rough figure below. \[\]
 

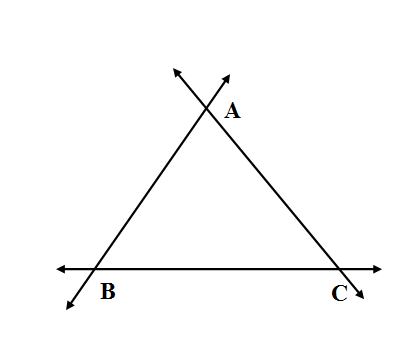
We see that we cannot draw any more straight line except $\overleftrightarrow{AB} , \overleftrightarrow{BC}$ , $\overleftrightarrow{AC}$ .

So, the correct answer is “3”.

Note: We can find the maximum number of lines we can draw using $n$ number of points using combination formula${}^{n}{{C}_{2}}=\dfrac{n\left( n-1 \right)}{2}$. Here $n=3$ so we have $^{3}{{C}_{2}}=\dfrac{3\cdot 2}{2}=3$. We can always draw a triangle and a circle passing through three non-collinear points. We can also find the number of angles subtended at the point of intersections $4{}^{n}{{C}_{2}}$.