Question

Switch S is closed at $ t = 0 $ , $ {I_{10}} $ is the current supplied by the battery just after closing the switch S. $ {Q_1} $ , $ {Q_2} $ and $ {Q_3} $ are the charges on the capacitors of $ 10\mu F $ , $ 20\mu F $ and $ 30\mu F $ in steady state respectively. $ {I_{20}} $ is the current supplied by the battery in the circuit at steady state. Choose the correct statement(s).

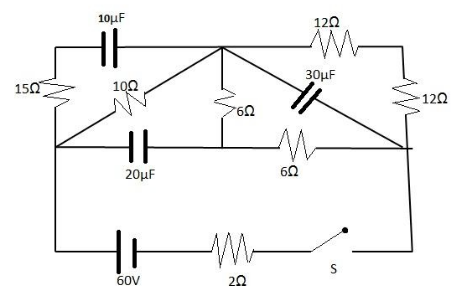
(A) $ {I_{10}} > {I_{20}} $
(B) $ {I_{10}} < {I_{20}} $
(C) $ {Q_1} < {Q_2} < {Q_3} $
(D) $ {Q_1} < {Q_3} < {Q_2} $

Answer 1

Hint: No current was flowing through the capacitors before the switch was closed at $ t = 0 $ . We know that current is the flow of charge.

Formula Used: The formulae used in the solution are given here.
Current $ I = C\dfrac{{dV}}{{dt}} $ , where $ C $ the capacitance in Farad and voltage across the capacitor is $ V $ .
Charge on the capacitor, $ Q = CV $ .

Complete Step by Step Solution
No flow of charge to and from the capacitors plates was zero, prior to $ t = 0 $ . Hence as charge on capacitor plates varies proportionally with the voltage across them, therefore voltage across them is zero before $ t = 0 $ . We can say that the capacitor was short circuited or it behaved as if it was being short circuited.
We know, current through capacitor, $ I $ and voltage across the capacitor, $ V $ , is related as
 $ I = C\dfrac{{dV}}{{dt}} $ , where $ C $ is the capacitance in Farad.
Following from the above, when the switch is turned on at $ t = 0 $ , the capacitor behaves as being short circuited , for the initial time being.
The circuit thus looks like,

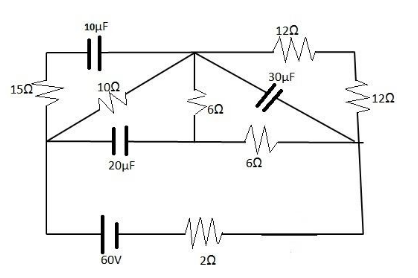
On solving, we see that the resistances $ 10\Omega $ , $ 6\Omega $ , $ 15\Omega $ , $ 6\Omega $ are in parallel. So equivalent resistance,
 $ \dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{10}} + \dfrac{1}{6} + \dfrac{1}{{15}} + \dfrac{1}{6} $
 $ \Rightarrow \dfrac{1}{{{R_{eq}}}} = \dfrac{1}{2} $ .
So equivalent resistance, $ {R_{eq}} = 2\Omega $ .
There is another resistance $ 2\Omega $ connected in series to the arrangement for which $ {R_{eq}} = 2\Omega $ .
Thus, resistance $ R = 4\Omega $ .
By Ohm’s Law, $ V = IR $ .
Thus, $ {I_{10}} = \dfrac{{60}}{4} = 15A $ .
At steady state, that is, after some time, the capacitor starts behaving like an open circuit.
Thus two $ 6\Omega $ resistors are in parallel with two $ 12\Omega $ resistors.
Equivalent resistance is thus,
 $ \dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{2 \times 6}} + \dfrac{1}{{2 \times 12}} $
 $ \Rightarrow \dfrac{1}{{{R_{eq}}}} = \dfrac{1}{8} $
S, equivalent resistance $ {R_{eq}} = 8\Omega $ .
There are two resistances $ 10\Omega $ and $ 2\Omega $ connected in series to the arrangement for which $ {R_{eq}} = 8\Omega $
By Ohm’s Law, $ V = IR $ .
At $ {I_{20}} = \dfrac{{60}}{{20}} = 3A. $
So $ {I_{20}} > {I_{10}} $ .
Hence Option A is correct.
Now charge on the capacitor, $ Q = CV $ .
Voltage across the $ 10\mu F $ capacitor at steady state= $ 30V $ .
 $ {Q_1} = 10\mu F \times 30 $ .
Voltage across the $ 20\mu F $ capacitor at steady state= $ 30V $ .
 $ {Q_2} = 20\mu F \times 42 $ .
Voltage across the $ 30\mu F $ capacitor at steady state= $ 30V $ .
 $ {Q_3} = 30\mu F \times 24 $ .
It is quite apparent, $ {Q_3} > {Q_2} > {Q_1} $ .
Hence Option D is also correct.

Note:
We can conclude that if voltage changes abruptly, current through the capacitor is spiked up. So, the tendency of the capacitor is to avoid the abrupt change in voltage across it.