Question

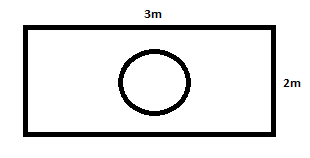
Suppose you drop a die at random on the rectangular region shown in fig. What is the probability that it will land inside the circle with diameter \[1m\]?
               

Answer 1

Hint: There is a problem to find the probability that land inside the circle with diameter \[1m\]
Probability is a type of ratio where we compare how many times an outcome can occur compared to all possible outcomes.
\[{\text{Probability = }}\dfrac{{\left( {{\text{The number of wanted outcomes}}} \right)}}{{\left( {{\text{The number of possible outcomes}}} \right)}}\]

Complete step-by-step answer:
The given figure is:
               

It is given that a die is dropped at random on the rectangular region shown in fig.
We need to determine the probability that it will land inside the circle with diameter \[1m\].
Here we use the area to find the probability.
Now we have the diameter of the circle is \[1m\].
Thus we get the radius of the circle is \[\dfrac{1}{2}m\] .
The area of the circle is
\[ \Rightarrow \pi {r^2}\]
Substituting the values in given,
\[ \Rightarrow \dfrac{{22}}{7} \times \dfrac{1}{2} \times \dfrac{1}{2}\]
\[ \Rightarrow \dfrac{{11}}{{14}}{m^2}\]
Again it is given that,
The length of the rectangle is \[3m\].
The breadth of the rectangle is \[2m\].
Thus the area of the rectangle is =\[3 \times 2 = 6{m^2}\]
Probability (P) that the die will land inside the circle
\[ \Rightarrow \dfrac{{\left( {{\text{The number of wanted outcomes}}} \right)}}{{\left( {{\text{The number of possible outcomes}}} \right)}}\]
Probability formula for the problem can be written as,
\[ \Rightarrow \dfrac{{{\text{The area of the circle}}}}{{{\text{the area of the rectangle}}}}\]
\[ \Rightarrow \dfrac{{\dfrac{{11}}{{14}}}}{{\dfrac{6}{1}}}\]
Simplifying we get,
\[ \Rightarrow \dfrac{{11}}{{14}} \times \dfrac{1}{6}\]
\[ \Rightarrow \dfrac{{11}}{{84}}\]
Hence we get, the probability that the die will land inside the circle with diameter \[1m\] is\[\dfrac{{11}}{{84}}\].

Note: A rectangle is a 2D shape in geometry, having four sides and four corners. Its two sides meet at right angles. Thus, a rectangle has four angles, each measuring \[90^\circ \]. The opposite sides of a rectangle have the same lengths and are parallel.
\[{\text{Area of the rectangle}}\] = \[Length \times breadth\]
A circle is a shape consisting of all points in a plane that are a given distance from a given point, the centre; equivalently it is the curve traced out by a point that moves in a plane so that its distance from a given point is constant.
Area of the circle is \[\pi {r^2}\].