Question

Suppose, we split a spherical surface into two parts by a circular loop. Now, a bar magnet is placed near the spherical system as shown in the figure. Through which of the two parts is the magnitude of the magnetic flux larger?

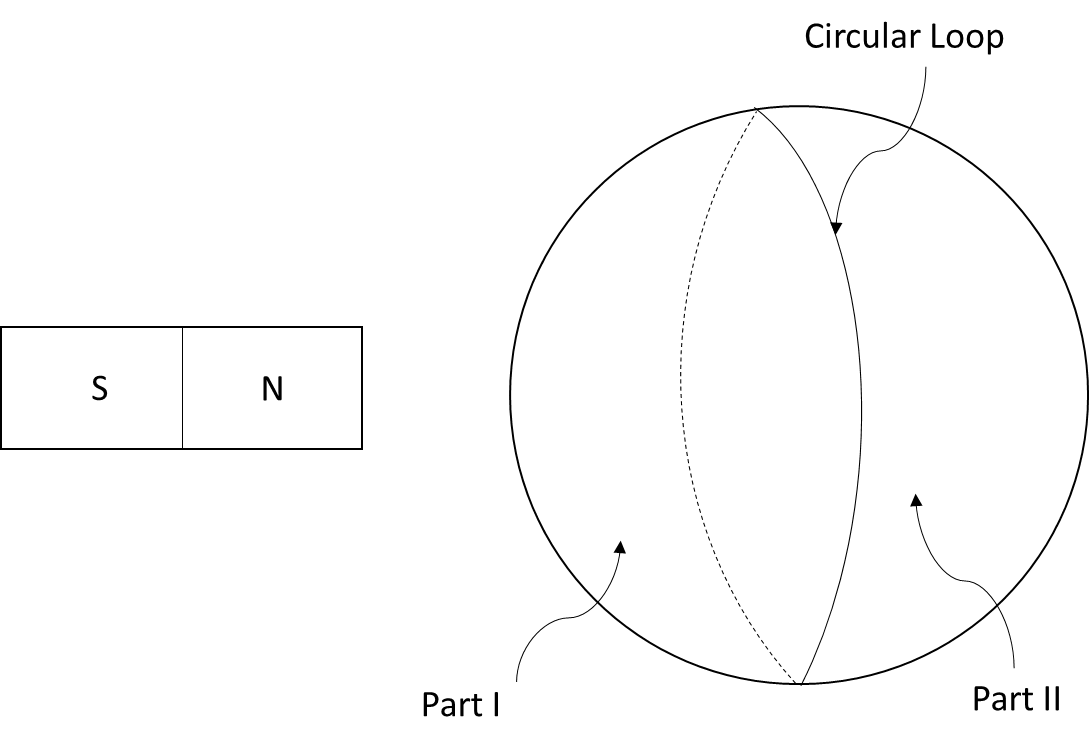
Answer 1

Hintthe above problem can easily be solved by the concept of magnetic flux. In order to solve, first we will calculate the flux through each of two parts by using the formula of magnetic flux. Since the magnetic field due to the bar magnet as well as the area will be the same in both the cases we can easily compare the magnitude of magnetic flux in the two parts of the sphere.

Complete step-by-step solution:
We know that formula for magnetic flux linked with area is given by
${\phi _m} = \overrightarrow B .\overrightarrow A $
Where,
${\phi _m}$ = Magnetic Flux
$\overrightarrow B $= Magnetic Field Vector
\[\overrightarrow A \] = Area Vector
Assume magnetic field produced by the bar magnet = \[\overrightarrow B \]
Assume Area vector of part I = \[\overrightarrow {{A_1}} \]
Assume Area vector of part II = \[\overrightarrow {{A_2}} \]
Flux induced in part I of the sphere = \[{\phi _{1m}}\]
Flux induced in part II of the sphere = \[{\phi _{2m}}\]

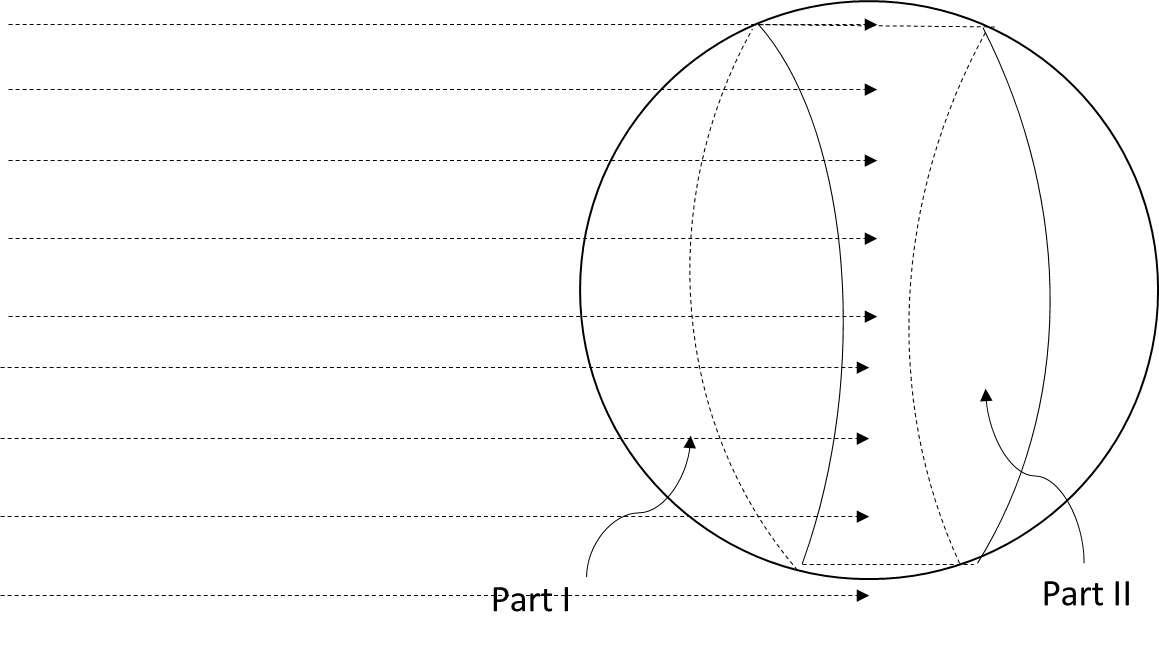
As clear from the above diagram it is clear that effective areas projected by the circular loop on the second part of the sphere are equal.
\[\overrightarrow {{A_1}} = \overrightarrow {{A_2}} \]
As dot product of two quantities is given by
\[\overrightarrow X \overrightarrow {.Y} = XY\cos \theta \]
$\therefore {\phi _{1m}} = B{A_1}\cos \theta $
Also the area vector is parallel to the magnetic field in both the parts
So the angle between area vector & Magnetic field is zero i.e. $\theta = 0$
${\phi _{1m}} = B{A_1}\cos {0^0}$
We can write
$\therefore $${\phi _{1m}} = B{A_1}$ (As $\cos 0 = 1$)
Similarly for other part we have
${\phi _{2m}} = \overrightarrow B .\overrightarrow {{A_2}} $
As dot product of two quantities is given by
\[\overrightarrow X \overrightarrow {.Y} = XY\cos \theta \]
$\therefore {\phi _{2m}} = B{A_2}\cos \theta $
Also $\theta = 0$
${\phi _{2m}} = B{A_2}\cos {0^0}$
${\phi _{2m}} = B{A_2}$ ( As $\cos 0 = 1$ )
On dividing ${\phi _{2m}}$ & ${\phi _{1m}}$
$\dfrac{{{\phi _{2m}}}}{{{\phi _{1m}}}} = \dfrac{{B{A_2}}}{{B{A_1}}}$
As \[\overrightarrow {{A_1}} = \overrightarrow {{A_2}} \]
$\therefore $${\phi _{1m}} = {\phi _{2m}}$
Hence the magnitude through both the parts of the spherical surface will be equal.
Additional Information: - The magnetic flux produced in a closed area only depends on the external magnetic field in which the area is placed in & also the area vector. It is basically the count of magnetic field lines passing through perpendicularly a closed area.

Note: This problem can also be solved from the concept that the total magnetic field entering the sphere is equal to the total magnetic field exiting. So the net flux is zero.
${\phi _{1m}} + {\phi _{2m}} = 0$
$\therefore $\[\left| {{\phi _{1m}}} \right| = \left| {{\phi _{2m}}} \right|\]