Question

Suppose the trigonometric ratio is $\sin x=\dfrac{9}{11}$ and$x\in \left( \dfrac{\pi }{2},\pi \right)$ , how do you find $\tan x$ and $\cos x$ ?

Answer 1

Hint: In these types of questions we should be very careful where $x$ lies. It means we should be alert about which quadrant $x$ lies in. We know that if $x\in \left( 0,\dfrac{\pi }{2} \right)$ then $x$ lies in the first quadrant. If $x\in \left( \dfrac{\pi }{2},\pi \right)$ , then $x$ lies in the second quadrant. If $x\in \left( \pi ,\dfrac{3\pi }{2} \right)$ then $x$ lies in the third quadrant. If $x\in \left( \dfrac{3\pi }{2},2\pi \right)$ , then $x$ lies in the fourth quadrant.

Complete step-by-step solution:
Let’s make use of the information provided in the hint.
The question mentioned $x\in \left( \dfrac{\pi }{2},\pi \right)$ . So we can conclude that $x$ belongs to the second quadrant.
Now we should know which trigonometric function is positive and which is negative in which quadrants.
We know that all the trigonometric functions are positive in the first quadrant.
$\sin x,\cos ecx$ are positive in the first quadrant and the second quadrant as well.
$\tan x,\cot x$ are positive in the first quadrant and the third quadrant as well.
$\cos x,\sec x$ are positive in the first quadrant and the fourth quadrant as well.
As $x$ lies in the second quadrant $\sin x$ are positive and $\tan x,\cos x$ must be negative.
Now let’s make use of the right angle triangle.
$\sin x=\dfrac{AB}{AC}=\dfrac{9}{11}$
From Pythagoras Theorem,
$\begin{align}
  & \Rightarrow {{\left( AB \right)}^{2}}+{{\left( BC \right)}^{2}}={{\left( AC \right)}^{2}} \\
 & \Rightarrow {{\left( BC \right)}^{2}}={{\left( AC \right)}^{2}}-{{\left( AB \right)}^{2}} \\
 & \Rightarrow {{\left( BC \right)}^{2}}=121-81=40 \\
 & \Rightarrow \left( BC \right)=\sqrt{40} \\
\end{align}$

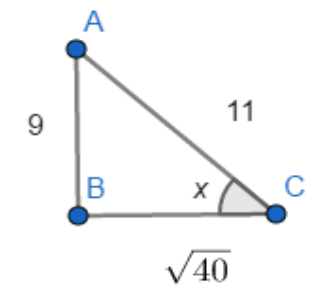
$\sin x=~\dfrac{AB}{AC}=\dfrac{9}{11}$
$\cos x=\dfrac{BC}{AC}=\dfrac{\sqrt{40}}{11}$
Since, $x$ is in the second quadrant, $\cos x$ must be negative.
$\therefore \cos =-\dfrac{\sqrt{40}}{11}$
$\tan x=\dfrac{AB}{BC}=\dfrac{9}{\sqrt{40}}$
Since $x$ is in the second quadrant, $\tan x$ must be negative.
$\therefore \tan x=\dfrac{AB}{BC}=\dfrac{-9}{\sqrt{40}}$.

Note: We should be careful with the signs. It is advisable to know the sign of each trigonometric function in each quadrant. We should also know the definition of $\sin x,\cos x,\tan x,\sec x,\cos ecx,\cot x$ Also be careful of the domain of $x$ as it defines the sign of each function.