Question

Suppose five of the nine vertices of a regular nine-sided polygon are arbitrarily chosen. Show that one can select four among these five such that they are the vertices of a trapezium.

Answer 1

Hint: Trapezium is a 2-dimensional geometric shape with 4 sides and 4 vertices. It has at least one pair of parallel sides. It has 4 sides and 4 vertices. The non-parallel sides are called legs.
Properties of a Trapezium:
The bases of the trapezium are parallel to each other.
No sides, angles and diagonals are congruent.
Now using the above information we can solve the given question.

Complete step by step solution:
Given
Five of the nine vertices of a regular nine - sided polygon are arbitrarily chosen................. i
We need to show that when we select four among these five such that they are the vertices of a trapezium.
We also know that for an isosceles trapezium the non-parallel sides of the trapezium are of equal length as well as their corresponding arcs.
Now let \[{\text{A, B, C, D, E, F, G, H}}\] be the corresponding points.
So let’s consider 3 cases:
Case 1: If four of the five points chosen are adjacent:
Let here \[{\text{A, B, C, D}}\] be adjacent as shown in the figure below:

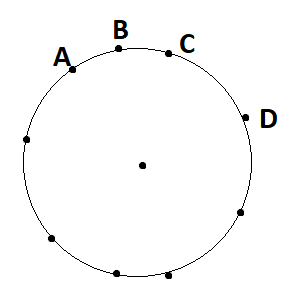
Here we can observe that:
\[\widehat {AB} = \widehat {BC} = \widehat {CD}......................\left( {ii} \right)\]
From (ii) it can be said that it forms an isosceles trapezium.
Case 2: Only three of the vertices are adjacent, say \[{\text{A, B, C }}\] then the remaining two must be among\[{\text{E, F, G, H}}\]. It can be shown in the figure below as:

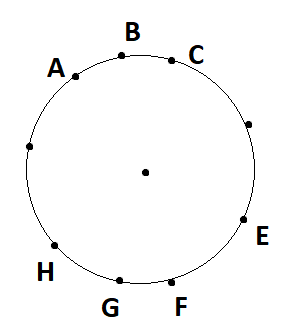
Here we can observe that \[\widehat {HA} = \widehat {CE}.......................\left( {iii} \right)\].
Such that $AHEC$ is an isosceles trapezium.
Case 3: Only two among the five are adjacent, say \[{\text{A, B}}\] . Then the remaining three are among \[{\text{D,E,F,G,H}}\]. It can be shown in the figure below as:

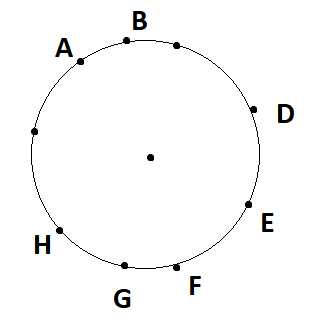
Here we can observe that $\widehat {HA} = \widehat {BD}.......................\left( {iv} \right)$.
Such that $AHDB$ is an isosceles trapezium.
Now from the above three cases it is observed that when we choose 5 among the 9 vertices of a regular nine-sided polygon, then some of the two must be adjacent.
Therefore we can conclude that by choosing any one of 5 among 9 will fall into one of the above three cases and result to be the vertices of a trapezium.
Note: Different types of trapezium:
The trapezium is classified into 3 types:
Isosceles trapezium: The legs or the non-parallel sides of the trapezium are of equal length
Scalene Trapezium: A trapezium with all the sides and angles of different measures
Right Trapezium: A right trapezium has at least two right angles
Also one should be thorough with the properties of polygons for solving questions similar to these.