Question

The curved surface area of a cone of slant height \[l\] and radius \[r\] is given by
A. \[\dfrac{1}{3}\dfrac{\pi }{{{r^2}}}\]
B. \[\pi rl\]
C. \[\pi r{l^2}\]
D. \[\dfrac{1}{3}\pi rl\]

Answer 1

Hint: We know that, the curved surface area \[ = \](Arc length of sector \[ \div \] Circumference of circle) \[ \times \]Area of circle.
At first, we will find the arc length of the sector, the circumference of the circle and the area of the circle.
Using the above formula and information we get the curved surface area.

Complete step-by-step solution:
Cone with slant height $l$ and radius $r$ is given by

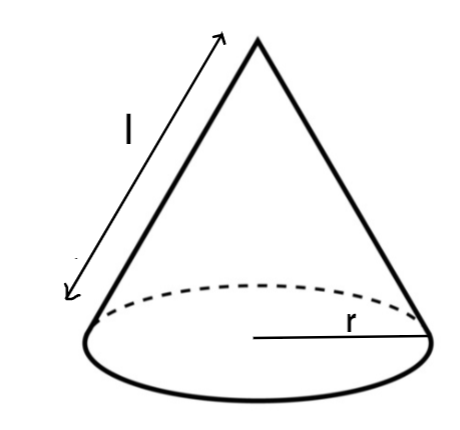
It is given that; the slant height of a cone is \[l\] and the radius is \[r\].
We have to find the curved surface area of the cone.
We know that, the curved surface area \[ = \](Arc length of sector \[ \div \]Circumference of circle) \[ \times \]Area of circle.
If a perpendicular cut is made from a point on the circumference of the base to the vertex and the cone is opened up, a sector of a circle with radius \[l\] is produced. Since the circumference of the base of the cone is \[2\pi l\], therefore the arc length of the sector of the circle is \[2\pi r\].
Now, substitute these values in the above given formula we get,
The curved surface area\[ = \dfrac{{2\pi r}}{{2\pi l}} \times \pi {l^2}\]
Simplifying we get,
The curved surface area\[ = \pi rl\]

Hence, the correct option is B.

Note: A cone is a shape formed by using a set of line segments or the lines which connects a common point, called the apex or vertex, to all the points of a circular base
The curved surface area is defined as the area of only curved surfaces, leaving the circular top and base.
The curved surface area of a right circular cone equals the perimeter of the base times one-half slant height.