Question

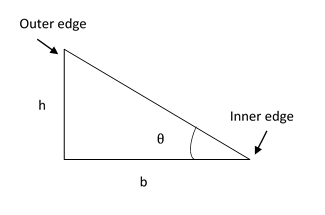
Suppose a vehicle moves on a curved road of width $b$ and radius of curvature $R$ with velocity $v$. Find the difference in elevation required between the outer edge and the inner edge of the road to counteract the centrifugal force acting on the vehicle.

A) $\dfrac{{{v^2}b}}{{Rg}}$
B) $\dfrac{{vb}}{{Rg}}$
C) $\dfrac{{v{b^2}}}{{Rg}}$
D) $\dfrac{{vb}}{{{R^2}g}}$

Answer 1

Hint: The vehicle moving on the curved road has a force acting on it that keeps the vehicle moving along the road (centripetal force) and an inertial force felt by the vehicle moving along the curved road (centrifugal). Both these forces are equal in magnitude but have opposite directions. The centripetal force is directed radially inward while the centrifugal force is directed radially outward.

Formula used:
The centripetal force of a body moving along a curved path of radius $r$with mass $m$ and velocity $v$ is given by, $\dfrac{{m{v^2}}}{r}$

Complete step by step answer:
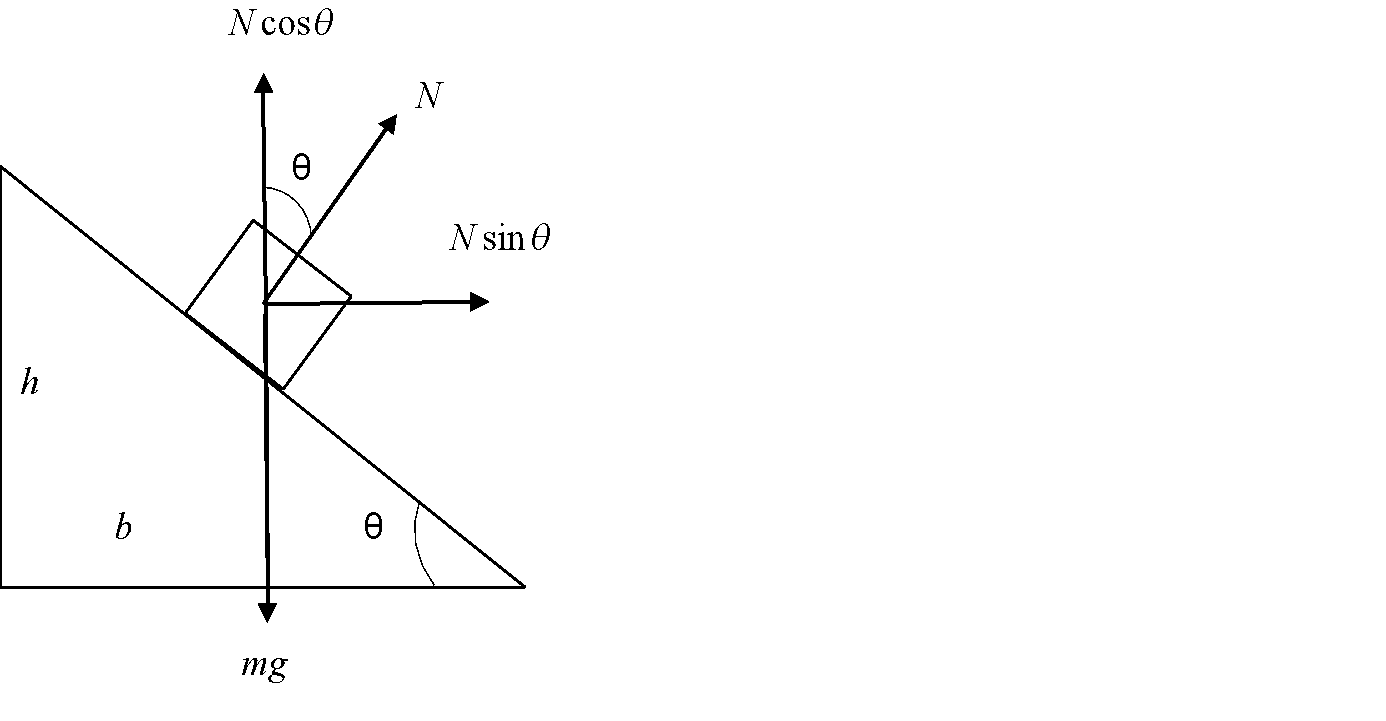
Step 1: Sketch a free body diagram of the problem and resolve the forces acting on the vehicle into its components.

Step 2: List the data obtained from the free body diagram.
The width of the road is $b$ and its radius of curvature is $R$.
The required difference in elevation between the outer edge and the inner edge is $h$.
The mass of the vehicle is $m$ and its velocity is $v$.
The forces acting on the body are - its weight $mg$ , the normal force $N$ which is resolved into its horizontal component $N\sin \theta $ and vertical component $N\cos \theta $ .

Step 3: Using the balancing condition find the required difference in elevation of $h$.
From the figure, we see that the weight of the body $mg$ is balanced by the vertical component of the normal force $N\cos \theta $ (no displacement along the vertical direction).
i.e., $N\cos \theta = mg$ ------- (1)
Also, the horizontal component of the normal force will provide the necessary centripetal force for the vehicle to move on the curved road.
So, $N\sin \theta = \dfrac{{m{v^2}}}{R}$ -------- (2)
Divide equation (2) by equation (1) to get, $\dfrac{{N\sin \theta }}{{N\cos \theta }} = \dfrac{{\left( {\dfrac{{m{v^2}}}{R}} \right)}}{{mg}}$
Simplifying the above equation we have, $\tan \theta = \dfrac{{{v^2}}}{{Rg}}$ ------- (3)
From the figure we have $\tan \theta = \dfrac{h}{b}$ -------- (4)
Equating the equations (3) and (4) we get, $\dfrac{h}{b} = \dfrac{{{v^2}}}{{Rg}}$
Now rearrange the above equation to get $h$.
i.e., $h = \dfrac{{{v^2}b}}{{Rg}}$

Therefore the difference in elevation required to counteract the centrifugal force is $h = \dfrac{{{v^2}b}}{{Rg}}$.

Note:
When a vector is resolved into its horizontal and vertical components the original vector makes an angle $\theta $ with its x component (horizontal component). Hence, the horizontal component of the vector is expressed in terms of $\cos \theta $ and the vertical component is expressed in terms of$\sin \theta $ as the vector along with its components constitutes a right triangle.