Question

Suppose a transversal cuts two distinct straight lines such that pairs of alternate angles are equal, then prove that the two lines are parallel to each other.

Answer 1

Hint: We are given two lines and one line intersecting the two lines. We will use the property of “vertically opposite angles are equal” to prove the lines are parallel. And we will add our given properties to prove the given statement.

Complete step-by-step answer:
Here we are to prove: \[AB\parallel CD\]
Proof:

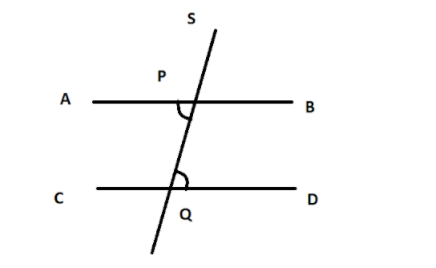
We have two straight lines AB and CD such that when transversal line intersects line AB at P and line CD at Q, a pair of alternate interior angles is equal.
 \[ \Rightarrow \;\;\angle APQ = \angle PQD\;{\text{ }}\;{\text{ }}\;{\text{ }}\;\] [Given] -- ( 1 )
When 2 lines intersect then we have, Vertically opposite angles are equal, hence we get,
 \[ \Rightarrow \;\;\angle APQ = \angle SPB\;{\text{ }}\;{\text{ }}\;{\text{ }}\;\] -- ( 2 )
From ( 1 ) and ( 2 ), we get
 \[ \Rightarrow \;\;\angle SPB = \angle PQD\]
If we take lines AB and CD, we can see that a pair of corresponding angles is equal.
This means line AB is parallel to CD.
 \[\therefore \;\;AB\parallel CD\;{\text{ }}\;{\text{ }}\;{\text{ }}\;{\text{ }}\;{\text{ }}\;\]
Hence, proved.

Note: If a set of 2 parallel lines, line l and line m, are crossed or cut by another line, line n, we say "a set of parallel lines are cut by a transversal. Each of the parallel lines cut by the transversal has 4 angles surrounding the intersection. These are matched in measure and position with a counterpart at the other parallel line.