Question

Sum of two binary numbers ${{\left( 1000010 \right)}_{2}}\text{and}{{\left( 11011 \right)}_{2}}$ is:
$\begin{align}
  & A.{{\left( 111101 \right)}_{2}} \\
 & B.{{\left( 111111 \right)}_{2}} \\
 & C.{{\left( 101111 \right)}_{2}} \\
 & D.{{(111001)}_{2}} \\
\end{align}$

Answer 1

Hint: The binary numbers are expressed in the base-2 numeral system. Sum of two binary numbers can be obtained adding one number to another number and get an answer. We need to remember the rules for the addition of binary numbers.

Complete step by step solution:
We know that the binary numbers are positional numeral systems employing 2 as the base and so requiring only two different symbols for its digits 0 and 1, instead of usual to different symbols needed in a decimal system. 0 and 1 are known as binary digits. Now, we have to find the sum of given numbers those are ${{\left( 1000010 \right)}_{2}}\text{and} {{\left( 11011 \right)}_{2}}$. We have to convert these binary numbers into the decimal system. For the first number, its decimal number can be given by ${{\left( 1000010 \right)}_{2}}$.
Now count these numbers one by one from right side, we get,
$\begin{align}
  & {{\left( 1000010 \right)}_{2}} \\
 & \downarrow \downarrow \downarrow \downarrow \downarrow \downarrow \downarrow \\
 & 6543210 \\
\end{align}$
As there is base of 2.
$\begin{align}
  & {{2}^{6}}+{{2}^{1}}=64+2 \\
 & ={{\left( 66 \right)}_{10}} \\
\end{align}$
So, ${{\left( 1000010 \right)}_{2}}={{\left( 66 \right)}_{10}}$ in decimal system for second number, its decimal number can be given by,
${{\left( 11011 \right)}_{2}}$ Similarly we get,
$\begin{align}
  & {{2}^{5}}+{{2}^{4}}+{{2}^{1}}+{{2}^{0}} \\
 & =32+16+2+1 \\
 & ={{(61)}_{10}} \\
\end{align}$
Therefore, ${{\left( 110011 \right)}_{2}}={{\left( 61 \right)}_{10}}$ in decimal system we have to add the decimal form of two numbers
${{\left( 66 \right)}_{10}}+{{\left( 61 \right)}_{10}}={{\left( 127 \right)}_{10}}$
Now, solve the L.C.M of 127
 

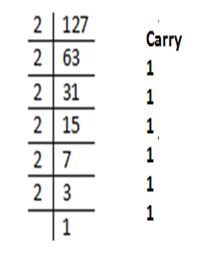
It is clear that the final answer will contain the 6 digits.
${{\left( 127 \right)}_{10}}={{\left( 111111 \right)}_{2}}$
${{\left( 111111 \right)}_{2}}$ Is the binary form of ${{(127)}_{10}}$

So the correct option is (b).

Additional information:
Modern day computers use binary numbers to operate- this is the fact well known to people studying computer science or to those using these machines on more than frequent basis.

Note:
There are three basic rules for adding binary numbers. It is advised to remember those rules in digital electronics; a binary number is expressed in the base- 2 numeral system which uses only two symbols: typically 0 and 1 the base – 2 numeral system is a positional notation with the radix 2.