Question

What is the sum of all exterior angles of a polygon?

Answer 1

Hint:
Here, we will find the sum of all exterior angles of a polygon.
We know that that sum of interior angle and sum of exterior angle is ${180^ \circ }$ .
Then, we will assume that the polygon has n sides.
Then after, Sum of all exterior angles + Sum of all interior angles $ = n \times {180^ \circ }$ .
Finally, to find, Sum of all exterior angles subtract Sum of all interior angles from $n \times {180^ \circ }$.

Complete step by step solution:
Here we know that, exterior angle + interior adjacent angle $ = {180^ \circ }$
Let us assume that polygon has n sides, then
Sum of all exterior angles + Sum of all interior angles $ = n \times {180^ \circ }$
Now, sum of all exterior angle $ = n \times {180^ \circ }$ - Sum of all interior angles
To find the sums of all interior angles we will follow the below method:
Let us consider a polygon of n sides.

Now, we will draw diagonals from point ${A_1}$ to all its opposite sides.

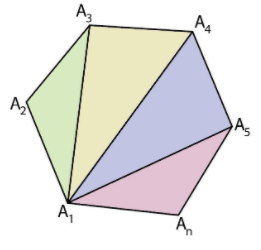
Thus, from the above diagram we get the sum of interior angles of the triangles as $\left( {n - 2} \right) \times {180^ \circ }$
So, the sum of all interior angles $ = \left( {n - 2} \right) \times {180^ \circ }$
 $ \Rightarrow $ Sum of all exterior angles
 $ = n \times {180^ \circ } - \left( {n - 2} \right) \times {180^{}}$
 $ = n \times {180^ \circ } - n \times {180^ \circ } + 2 \times {180^ \circ }$
 $ = {180^ \circ }n - {180^ \circ }n + {360^ \circ }$

Hence, we conclude that the sum of exterior angles of polygon having n sides is ${360^ \circ }$

Note:
Polygon: In geometry, a polygon is a plane figure that is described by a finite number of straight-line segments connected to form a closed polygon chain or polygonal circuit. The solid plane region, the bounding circuit, or the two together, may be called a polygon.