Question

State true or false: “Pair of vertically opposite angles are always supplementary.” \[\]
A. True \[\]
B. False \[\]

Answer 1

Hint: We recall the four angles subtended at the point of intersection of two lines. We recall the definitions of linear angles, pair of vertically opposite angles, and supplementary angles. We use the fact that pairs of vertically opposite angles have equal measure and check the condition for which they will be supplementary.

Complete step-by-step solution
We know that two lines can at most intersect each other at one point and when they intersect we get four angles subtended at the point of intersection. The pair of angles that one side on a line or ray is called linear pair and the pair of angles, which do not have any common ray or side are called vertically opposite angles.
Let $\overleftrightarrow{AB}$ and $\overleftrightarrow{CD}$ be two straight lines that intersect each other at the point O. We have the rough figure below.\[\]

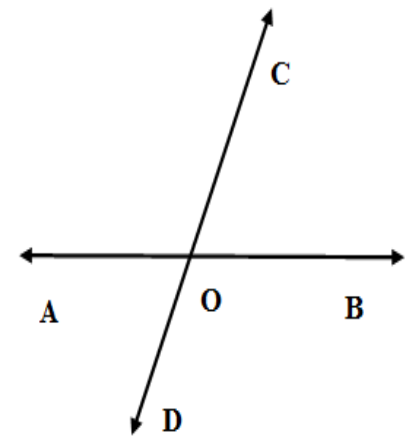
Here the four angles subtended at the point $O$ are $\angle AOC,\angle BOC,\angle AOD,\angle BOD$. The angles $\angle AOC$ and $\angle BOD$ do not share any common ray. So they are vertically opposite angles. Similarly, $\angle BOC$ and $\angle AOD $ do not share any common ray and hence are vertically opposite angles. The pair of angles $\angle AOC,\angle AOD$ and $\angle BOC,\angle BOD$ have a common side on the line $\overleftrightarrow{AB}$. So they are linear pairs. Similarly, $\angle AOC,\angle BOC$ and $\angle AOB,\angle AOD$ are linear pairs of angles. \[\]
We know that we call two angles supplementary when their sum of measure is ${{180}^{\circ }}$. We know that the sum of linear pair of angles is always ${{180}^{\circ }}$ and hence they are supplementary. We know that vertically opposite angles are always equal. \[\]
Let us take the sum of vertically opposite angles $\angle AOC$ and $\angle BOD$ whose measures equal $\angle AOC=\angle BOD$. We assume that,
\[\begin{align}
  & \angle AOC+\angle BOD={{180}^{\circ }} \\
 & \Rightarrow \angle AOC+\angle AOC={{180}^{\circ }} \\
 & \Rightarrow 2\angle AOC={{90}^{\circ }} \\
 & \Rightarrow \angle AOC=\dfrac{{{180}^{\circ }}}{2}={{90}^{\circ }} \\
\end{align}\]
This only possible when vertically opposite angles will be supplementary when they are right angle otherwise will not be supplementary. So the given statement “Pair of vertically opposite angles are always supplementary” is false. \[\]

Note: We note that linear pairs of angles lie on a line and share a common vertex, pair vertically opposite angles share a common vertex but two supplementary angles may not share either a common line or common vertex, for example, adjacent angles of a parallelogram.