Question

State true or false:
Every parallelogram is a trapezium.
(a) True
(b) False

Answer 1

Hint: First, we should know the definition and properties of parallelogram and Trapezium. After knowing this, we have to see if the property of parallelogram is fulfilled in the property of trapezium or not. Thus, we will get our answer.

Complete step-by-step answer:
Here, we will first understand the definition and properties of parallelogram and trapezium.
Parallelogram: It is also a flat shaped figure which four sides out of which opposite sides are equal in length and opposite angles are of same measure. Diagram is as shown below:
 

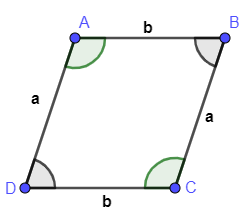
Also, also $\angle A=\angle C$ and $\angle B=\angle D$ are equal also, sides $AD=BC$ and $AB=CD$ .
Trapezium: It consists of four sides and only one pair of sides is parallel to another.
 

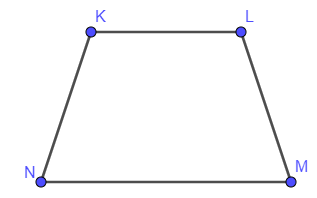
Here, only KL is parallel to NM denoted as $KL\parallel NM$ .
So, now if we compare property of parallelogram with trapezium it will not match i.e. in parallelogram there are two sets of sides which are parallel and also equal in measure while in trapezium only one side is parallel but not of the same measure.
Thus, every parallelogram is not a trapezium.
Hence, option (b) is correct.

Note: To solve this type of problem students should know all the properties of quadrilaterals like parallelogram, rhombus, rectangle, square, trapezium. Suppose if any one property of parallelogram is matched to property of trapezium then we have to check another property of parallelogram. Do not make assumptions by taking any one property if matched otherwise the answer will be incorrect. Thus, the key point is to find which quadrilateral properties match with another quadrilateral.