
State the law of parallelogram of vector addition and find the magnitude and direction of the resultant of vectors P and Q inclined at an angle $\theta$ with each other. What happens when $\theta=0^{\circ}$ and $\theta = 90^{\circ}$.
Answer
585.9k+ views
Hint: At First sketch out how your vectors and its resultant would look on a parallelogram. Then label the angle between the two vectors as $\theta$ and between one of the vectors and the resultant as $\phi$, and establish a geometrical understanding of the arrangement of the vectors. Once you do this, play around with trigonometric identities to obtain the values of $sin\theta$ and $cos\theta$ and make sure to include the magnitudes of the participating vectors in the relations that you obtain. Also, remember to use the Pythagoras theorem to ultimately find the resultant magnitude, and the resultant direction will follow from here and you should arrive at it in terms of $tan \phi$.
Formula Used:
Parallelogram law of vector addition for the resultant of two vectors: $\vec{R} = \vec{P} +\vec{Q}$, where $\vec{P}$ and $\vec{Q}$ are two vector quantities that can be represented as the adjacent sides of a parallelogram.
Magnitude of the resultant vector $|R| = \sqrt{|P|^2 +2|P||Q|\;cos\theta +|Q|^2}$ , where $|P|$ and $|Q|$ are the magnitudes of vectors $\vec{P}$ and $\vec{Q}$, and $\theta$ is the angle between vectors $\vec{P}$ and $\vec{Q}$.
Direction of the resultant $\phi = tan^{-1}\left(\dfrac{|Q|\;sin\theta}{|P|+|Q|\;cos\theta}\right)$
Complete step-by-step solution:
Let us begin with the parallelogram law of vector addition.
The law states that if two vector quantities are represented by two adjacent sides of a parallelogram then the resultant of these two vectors will be the diagonal of the parallelogram.
Let us try and understand how this works:
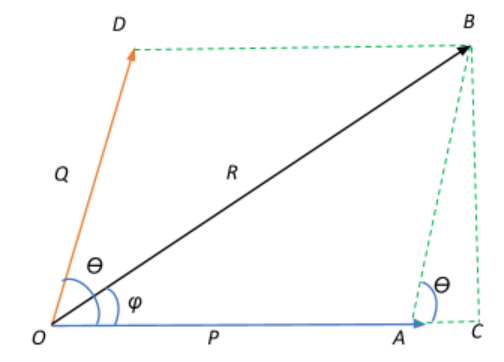
Let the two vectors $\vec{P}$ and $\vec{Q}$ acting from the same point O be represented both in magnitude and direction as two adjacent sides OA and OD of a parallelogram OABD.
Let the angle between the two vectors be $\theta$.
According to our definition of the parallelogram law of vector addition, the diagonal of the parallelogram OB represents the resultant of $\vec{P}$ and $\vec{Q}$. Thus, let the resultant of the two vectors be represented by $\vec{R}$ that is at an angle $\phi$ with $\vec{P}$.
$\vec{R} = \vec{P} +\vec{Q}$
The sides $AB=OD = |Q|$ and $OA=BD=|P|$ and diagonal $OB = |R|$
Consider the right angle triangle OBC. From the Pythagorean theorem:
$OB^2 = OC^2+BC^2 = (OA+AC)^2 +BC^2$
Consider the triangle ABC:
$cos\theta = \dfrac{AC}{AB} \Rightarrow AC = AB\;cos\theta = OD\;cos\theta \Rightarrow AC = |Q|\;cos\theta$
Also $sin\theta = \dfrac{BC}{AB} \Rightarrow BC=AB\;sin\theta = OD\;sin\theta \Rightarrow BC = |Q|\;sin\theta$
Substituting the AC and BC expressions in the $OB^2$ Pythagorean theorem, we get:
$|R|^2 = (|P| + |Q|\;cos\theta)^2 + (|Q|\;sin\theta)^2 = |P|^2 +2|P||Q|\;cos\theta +|Q|^2(cos^2\theta +sin^2\theta) = |P|^2 +2|P||Q|\;cos\theta +|Q|^2$
Therefore, the magnitude of the resultant
$|R| = \sqrt{|P|^2 +2|P||Q|\;cos\theta +|Q|^2}$
Now let us find the direction of the resultant:
From triangle ABC $tan\phi = \dfrac{BC}{OC} = \dfrac{BC}{OA+AC} = \dfrac{|Q|\;sin\theta}{|P|+|Q|\;cos\theta}$
Therefore, the direction of the resultant with respect to $\vec{P}$ is given by
$\phi = tan^{-1}\left(\dfrac{|Q|\;sin\theta}{|P|+|Q|\;cos\theta}\right)$
We have thus obtained the magnitude and direction of the resultant $\vec{R}$
Now, when $\theta = 0^{\circ}$:
$|R| = \sqrt{|P|^2 +2|P||Q|\;cos\;0 +|Q|^2} = \sqrt{|P|^2 +2|P||Q| +|Q|^2} = \sqrt{(|P|+|Q|)^2} \Rightarrow |R| = |P| +|Q| $
$\phi = tan^{-1}\left(\dfrac{|Q|\;sin\;0}{|P|+|Q|\;cos 0}\right) = tan^{-1}(0) = 0$
Thus, in this case, the magnitude of the resultant vector will be the sum of the magnitudes of the adjacent vectors and the the resultant lies in the direction of $\vec{P}$
And finally, when $\theta = 90^{\circ}$:
$|R| = \sqrt{|P|^2 +2|P||Q|\;cos\;90 +|Q|^2} = \sqrt{|P|^2 +|Q|^2} = \sqrt{(|P|^2+|Q|^2)}$
$\phi = tan^{-1}\left(\dfrac{|Q|\;sin\;90}{|P|+|Q|\;cos\;90}\right) = tan^{-1}\left(\dfrac{Q}{P}\right)$
$\left(since\; sin\;0^{\circ} = 0, cos\; 0^{\circ} = 1, sin\;90^{\circ} = 1, cos\;90^{\circ} = 0, tan\;0^{\circ} = 0\right)$
Note: It is important to notice that the direction of the resultant that we have obtained in our above derivation is the angle that the resultant makes with only the vector $\vec{P}$. Alternatively, you can find the angle that the resultant makes with the vector $\vec{Q}$ by taking the angle to be $\theta -\phi$, as is evident from our above diagram.
Formula Used:
Parallelogram law of vector addition for the resultant of two vectors: $\vec{R} = \vec{P} +\vec{Q}$, where $\vec{P}$ and $\vec{Q}$ are two vector quantities that can be represented as the adjacent sides of a parallelogram.
Magnitude of the resultant vector $|R| = \sqrt{|P|^2 +2|P||Q|\;cos\theta +|Q|^2}$ , where $|P|$ and $|Q|$ are the magnitudes of vectors $\vec{P}$ and $\vec{Q}$, and $\theta$ is the angle between vectors $\vec{P}$ and $\vec{Q}$.
Direction of the resultant $\phi = tan^{-1}\left(\dfrac{|Q|\;sin\theta}{|P|+|Q|\;cos\theta}\right)$
Complete step-by-step solution:
Let us begin with the parallelogram law of vector addition.
The law states that if two vector quantities are represented by two adjacent sides of a parallelogram then the resultant of these two vectors will be the diagonal of the parallelogram.
Let us try and understand how this works:

Let the two vectors $\vec{P}$ and $\vec{Q}$ acting from the same point O be represented both in magnitude and direction as two adjacent sides OA and OD of a parallelogram OABD.
Let the angle between the two vectors be $\theta$.
According to our definition of the parallelogram law of vector addition, the diagonal of the parallelogram OB represents the resultant of $\vec{P}$ and $\vec{Q}$. Thus, let the resultant of the two vectors be represented by $\vec{R}$ that is at an angle $\phi$ with $\vec{P}$.
$\vec{R} = \vec{P} +\vec{Q}$
The sides $AB=OD = |Q|$ and $OA=BD=|P|$ and diagonal $OB = |R|$
Consider the right angle triangle OBC. From the Pythagorean theorem:
$OB^2 = OC^2+BC^2 = (OA+AC)^2 +BC^2$
Consider the triangle ABC:
$cos\theta = \dfrac{AC}{AB} \Rightarrow AC = AB\;cos\theta = OD\;cos\theta \Rightarrow AC = |Q|\;cos\theta$
Also $sin\theta = \dfrac{BC}{AB} \Rightarrow BC=AB\;sin\theta = OD\;sin\theta \Rightarrow BC = |Q|\;sin\theta$
Substituting the AC and BC expressions in the $OB^2$ Pythagorean theorem, we get:
$|R|^2 = (|P| + |Q|\;cos\theta)^2 + (|Q|\;sin\theta)^2 = |P|^2 +2|P||Q|\;cos\theta +|Q|^2(cos^2\theta +sin^2\theta) = |P|^2 +2|P||Q|\;cos\theta +|Q|^2$
Therefore, the magnitude of the resultant
$|R| = \sqrt{|P|^2 +2|P||Q|\;cos\theta +|Q|^2}$
Now let us find the direction of the resultant:
From triangle ABC $tan\phi = \dfrac{BC}{OC} = \dfrac{BC}{OA+AC} = \dfrac{|Q|\;sin\theta}{|P|+|Q|\;cos\theta}$
Therefore, the direction of the resultant with respect to $\vec{P}$ is given by
$\phi = tan^{-1}\left(\dfrac{|Q|\;sin\theta}{|P|+|Q|\;cos\theta}\right)$
We have thus obtained the magnitude and direction of the resultant $\vec{R}$
Now, when $\theta = 0^{\circ}$:
$|R| = \sqrt{|P|^2 +2|P||Q|\;cos\;0 +|Q|^2} = \sqrt{|P|^2 +2|P||Q| +|Q|^2} = \sqrt{(|P|+|Q|)^2} \Rightarrow |R| = |P| +|Q| $
$\phi = tan^{-1}\left(\dfrac{|Q|\;sin\;0}{|P|+|Q|\;cos 0}\right) = tan^{-1}(0) = 0$
Thus, in this case, the magnitude of the resultant vector will be the sum of the magnitudes of the adjacent vectors and the the resultant lies in the direction of $\vec{P}$
And finally, when $\theta = 90^{\circ}$:
$|R| = \sqrt{|P|^2 +2|P||Q|\;cos\;90 +|Q|^2} = \sqrt{|P|^2 +|Q|^2} = \sqrt{(|P|^2+|Q|^2)}$
$\phi = tan^{-1}\left(\dfrac{|Q|\;sin\;90}{|P|+|Q|\;cos\;90}\right) = tan^{-1}\left(\dfrac{Q}{P}\right)$
$\left(since\; sin\;0^{\circ} = 0, cos\; 0^{\circ} = 1, sin\;90^{\circ} = 1, cos\;90^{\circ} = 0, tan\;0^{\circ} = 0\right)$
Note: It is important to notice that the direction of the resultant that we have obtained in our above derivation is the angle that the resultant makes with only the vector $\vec{P}$. Alternatively, you can find the angle that the resultant makes with the vector $\vec{Q}$ by taking the angle to be $\theta -\phi$, as is evident from our above diagram.
Recently Updated Pages
Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Master Class 11 Physics: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Class 11 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Explain zero factorial class 11 maths CBSE

State the laws of reflection of light

Difference Between Prokaryotic Cells and Eukaryotic Cells

10 examples of friction in our daily life




