Question

State Kirchhoff’s voltage law.

Answer 1

Hint: Here, in the question, we need to define and explain the Kirchhoff’s law. Kirchhoff’s law is divided into two sub-parts, i.e., Kirchhoff’s current law and Kirchhoff’s voltage law. We will limit our discussion here to Kirchhoff's voltage law only.

Complete step by step answer:
According to Kirchhoff’s voltage law, the algebraic sum of the voltage drop across all the elements in a closed circuit equals to zero. In other words, Kirchhoff's law is the conservation of energy in a closed circuit. Mathematically $\sum V = 0$.
Let us take an example to better understand the topic.
Consider a closed circuit such that a resistor of resistance R, an inductor of inductance L, and a capacitor of capacitance C are connected in series across an AC voltage source, V. Also, consider a current I flowing in the closed circuit.

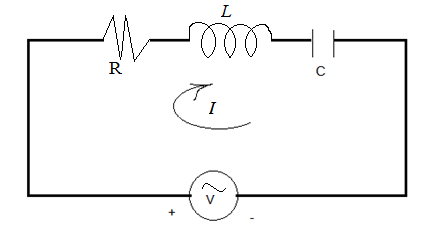
In the shown figure, let us apply the Kirchhoff’s voltage rule as:
$
  V - {V_R} - {V_L} - {V_C} = 0 \\
   \Rightarrow V - IR - L\dfrac{{dI}}{{dt}} - \dfrac{1}{C}\int {Idt} = 0 \\
   \Rightarrow V = IR + L\dfrac{{dI}}{{dt}} + \dfrac{1}{C}\int {Idt} \\
$
Hence, we can see that the energy remains conserved in the given circuit.

Note:
It is interesting to note here that the full name of Kirchhoff’s voltage law is Gustav Kirchhoff’s Voltage Law, in which Gustav Kirchhoff is the name of the scientist who discovered this law. Moreover, it is advised to the students to be aware while using the current sign convention and it varies from person-to-person.