Question

State clearly how an unpolarised light gets linearly polarised when passed through a polaroid.
a) Unpolarised light of intensity ${{I}_{0}}$ is incident on a polaroid ${{P}_{1}}$ which is kept near another polaroid ${{P}_{2}}$ whose pass axis is parallel to that of ${{P}_{1}}$. How will the intensities of light, ${{I}_{1}}$ and ${{I}_{2}}$, transmitted by the polaroids ${{P}_{1}}$ and ${{P}_{2}}$ respectively, change on rotating ${{P}_{1}}$ without disturbing ${{P}_{2}}$?
b) Write the relation between the intensities ${{I}_{2}}$ and ${{I}_{1}}$.

Answer 1

Hint: An unpolarised light oscillates in all possible directions. A linearly polarised light oscillates in a single direction. When polarised light falls on an analyser, the intensity of polarised light is given by Malu’s law.

Complete answer:
Polarisation refers to the property of waves that talks about the geometrical orientation of oscillations. An unpolarised light, like a transverse wave, oscillates in all possible directions whereas a linearly polarised light oscillates in a single direction. The optical sheet used to change unpolarised light to polarised light is termed as a polariser or a polaroid. The following diagram explains the above explanation.

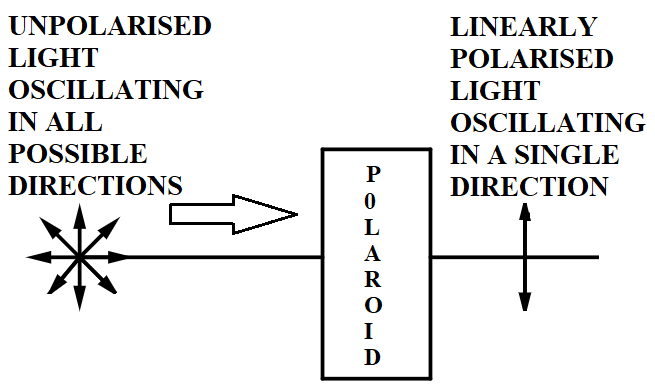
When an unpolarised light of intensity ${{I}_{0}}$ passes through a polaroid, its intensity reduces to half. If we call this intensity ${{I}_{1}}$, then,
${{I}_{1}}=\dfrac{{{I}_{0}}}{2}$
Let this be equation 1.
A polarised light can also be passed through a polaroid. In this case too, the intensity of the polarised light changes. This change in intensity is given by Malu’s law. Malu’s law states that
${{I}_{2}}={{I}_{1}}{{\cos }^{2}}\theta $
where
${{I}_{2}}$ is the intensity of polarised light after passing through the polaroid
${{I}_{1}}$ is the intensity of polarised light before passing through the polaroid
$\theta $ is the angle between the light’s initial polarisation direction and the axis of the polaroid
Coming to the question, at first, an unpolarised light of intensity ${{I}_{0}}$ passes through a polaroid ${{P}_{1}}$. The polaroid ${{P}_{1}}$ changes the unpolarised light to a linearly polarised light of intensity ${{I}_{1}}$. From equation 1, we know that
${{I}_{1}}=\dfrac{{{I}_{0}}}{2}$
Now, this linearly polarised light of intensity ${{I}_{1}}$ is allowed to pass through another polaroid ${{P}_{2}}$, kept near ${{P}_{1}}$, with its pass axis parallel to that of ${{P}_{1}}$. In this case, the second polaroid is also called an analyser. So, from now on, let us call ${{P}_{2}}$, analyzer.
The intensity of linearly polarised light ${{I}_{1}}$ changes after passing through the analyser and is given by Malu’s law. So, from equation 2, we have
${{I}_{2}}={{I}_{1}}{{\cos }^{2}}\theta $
where
$\theta $ is the angle between the linearly polarised light and the axis of the analyser.
The following diagram can be used to clarify the above explanation.

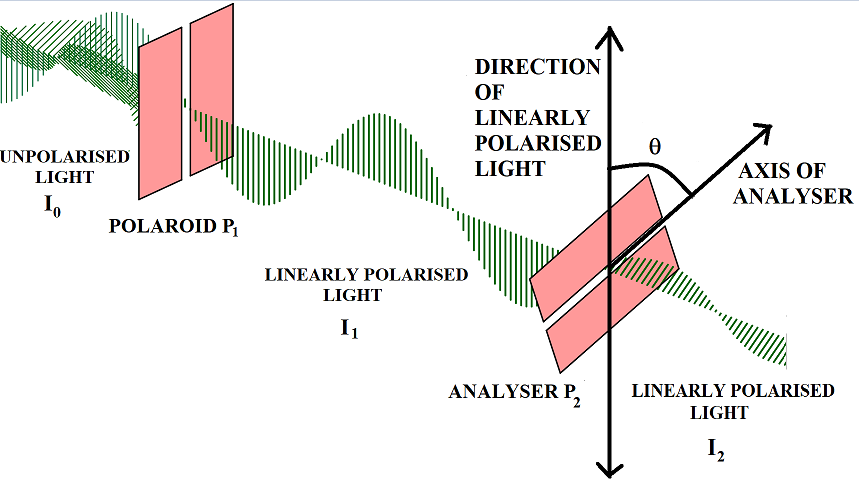
Therefore,
a) When ${{P}_{1}}$ is rotated without disturbing ${{P}_{2}}$, the intensity of light coming from ${{P}_{1}}$ remains the same$(=\dfrac{{{I}_{0}}}{2})$ and the intensity of light coming from ${{P}_{2}}$ is equal to ${{I}_{1}}{{\cos }^{2}}\theta $.
b) The relationship between intensities ${{I}_{1}}$ and ${{I}_{2}}$ is given by
${{I}_{2}}={{I}_{1}}{{\cos }^{2}}\theta $

Note:
Malu’s law can also be used to explain the change in intensity of an unpolarised light, when passed through a polaroid. Suppose ${{I}_{0}}$ is the intensity of unpolarised light and ${{I}_{1}}$ be the intensity of polarised light after passing through a polaroid,
${{I}_{1}}={{I}_{0}}{{\cos }^{2}}\theta $
where
$\theta $ is the angle between the direction of unpolarised light and the axis of polaroid.
Now, we know that an unpolarised light oscillates in all possible directions. Hence, the average value of ${{\cos }^{2}}\theta $ is taken as$\dfrac{1}{2}$. Substituting this value in the above expression, we have
${{I}_{1}}={{I}_{0}}{{\cos }^{2}}\theta ={{I}_{0}}\left( \dfrac{1}{2} \right)=\dfrac{{{I}_{0}}}{2}$
Therefore, the intensity of an unpolarised light, oscillating in all possible directions, reduces to half when passed through a polaroid.