Question

State Brewster’s Law? Prove that if the light is incident at the angle of polarization, the reflected and the refracted rays are mutually perpendicular.

Answer 1

Hint: When light falls on an interface between two transparent media at a particular angle called the polarization angle or the Brewster angle, the light will completely pass through into the second medium without any reflection if the light incident is linearly polarized. If the light incident is unpolarized, then the reflected will be completely polarized. This only happens when the refracted and the reflected rays are mutually perpendicular.

Equation Used:
Brewster’s Law states that the tangent to the angle of polarization is equal to the refractive index of the reflecting medium with respect to the surroundings.
$\tan \left( {{i}_{p}} \right)=\dfrac{{{n}_{2}}}{{{n}_{1}}}$
Snell’s Law: the ratio of the refractive index of the second medium to the refractive index of the first medium is equal to the ratio of the sine of the angle of incidence to the sine of the angle of refraction.
$\dfrac{\sin \left( i \right)}{\sin \left( r \right)}=\dfrac{{{n}_{2}}}{{{n}_{1}}}$

Complete step-by-step answer:
We know that a light travelling from one medium to another is refracted when it enters the second medium. There is also a small amount of light that is being reflected off this surface. When unpolarized light is incident on the boundary separating two optical mediums, most of the light incident gets refracted into the second medium while the rest is reflected back into the first medium. At an angle called the angle of polarization or Brewster’s angle, the reflected light will be completely polarized.

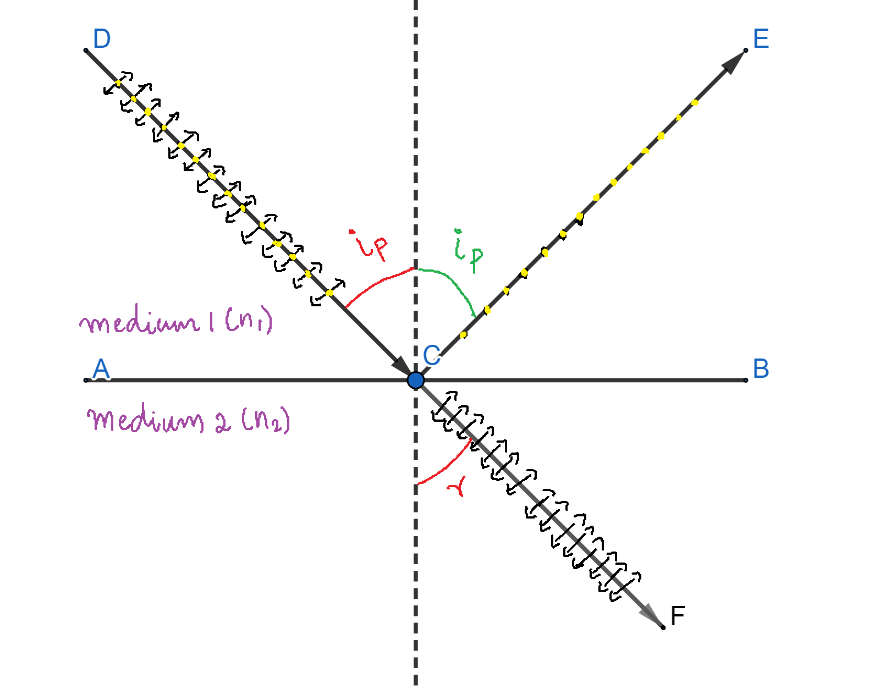
Brewster’s Law states that the tangent to the angle of polarization is equal to the refractive index of the reflecting medium with respect to the surroundings. The reflecting medium is the medium 2 in our discussion and surroundings is the medium 1. So, we can write Brewster’s Law mathematically as,
$\tan \left( {{i}_{p}} \right)=\dfrac{{{n}_{2}}}{{{n}_{1}}}$ … equation (1)
Where, ${{i}_{p}}$ is the polarizing angle.
${{n}_{1}}$ is the refractive index of the first medium.
${{n}_{2}}$ is the refractive index of the second medium.
We know from Snell’s Law that the ratio of the refractive index of the second medium to the refractive index of the first medium is equal to the ratio of the sine of the angle of incidence to the sine of the angle of refraction.
$\dfrac{\sin \left( i \right)}{\sin \left( r \right)}=\dfrac{{{n}_{2}}}{{{n}_{1}}}$ … equation (2)
Comparing equation (1) and (2), we can write,
$\tan \left( {{i}_{p}} \right)=\dfrac{\sin \left( i \right)}{\sin \left( r \right)}$
We can rewrite this as,
$\dfrac{\sin \left( {{i}_{p}} \right)}{\cos \left( {{i}_{p}} \right)}=\dfrac{\sin \left( i \right)}{\sin \left( r \right)}$
Comparing numerator and denominator on both sides, we get,
$\sin \left( {{i}_{p}} \right)=\sin \left( i \right)$ … equation (3)
$\cos \left( {{i}_{p}} \right)=\sin \left( r \right)$ … equation (4)
From equation (3), it is clear that, ${{i}_{p}}=i$, the angle of incidence, in this case, is the angle of polarization.
From equation (4), it is clear that,
$\cos \left( {{i}_{p}} \right)=\sin \left( r \right)$
$\Rightarrow \sin \left( 90-{{i}_{p}} \right)=\sin \left( r \right)$
$\therefore r=90-{{i}_{p}}$ … equation (5)
From the figure given above,
If $r=90-{{i}_{p}}$, then the angle $\angle BCF={{i}_{p}}\text{ }(\because \angle r+\angle BCF={{90}^{\circ }})$.
Also, from the figure given above, $\angle ECB={{90}^{\circ }}-{{i}_{p}}$
$\therefore \angle ECF=\angle ECB+\angle BCG$
$\Rightarrow \angle ECF=\left( {{90}^{\circ }}-{{i}_{p}} \right)+\left( {{i}_{p}} \right)$
$\therefore \angle ECF={{90}^{\circ }}$
So, in this case, the reflected and the refracted rays are perpendicular to each other.
So, when the light is incident at a polarization angle or Brewster’s angle, then the refracted and the reflected rays will be perpendicular to each other.

Note: There are two types of polarization when we are considering the plane of incidence, which is a plane in which the light propagates before and after refraction or reflection. Components of the electric field parallel to this plane of incidence are called the p- polarized light and when the electric field is perpendicular to the plane of incidence are called s-polarized light.
Electric dipoles on the boundary of the two mediums are responsible for the polarization of light. These electric dipoles absorb the light falling on it and re-emit these light. The refraction and reflection of light at the interface of the two mediums are managed by the electric dipoles present. The dipoles that produce the transmitted (refracted) light oscillate in the polarization direction of that light. These same oscillating dipoles also generate the reflected light.