Question

State and explain the Lenz law of induced EMF.

Answer 1

Hint: Here we have to discuss induced EMF which is induced due to the relative motion between the magnet and current-conducting coil hence we have to relate or understand this law in reference to magnetic field.

Complete step by step answer:
According to Lenz law, the magnetic field created by induced current opposes the initial changing magnetic field which produced it. The direction of this current flow due to the initial changing magnetic field is always given by Fleming’s right-hand rule.
According to Lenz law, if a magnet is to be a move towards a current-carrying coil or vice-versa then the magnetic field produced works in such a way that it always opposes the motion of the current-carrying coil.

Additional information:
There are two cases of Lenz law:

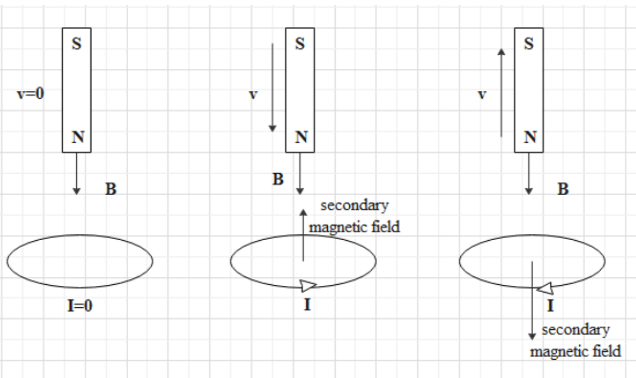
The first case: When a magnet is moving towards the coil
When the north pole of the magnet moves towards the pole no number of magnetic field lines through the coil or the magnetic flux through the coil changes and according to Lenz’s law the induced magnetic field will oppose this change in flux. The only way to do this is that the coil side towards the magnet should attain the north polarity and then the coil will repel the magnet.

Second case: When a magnet is moving away from the coil
When the north pole of the magnet is moving away from the coil, the number of magnetic field lines of the magnetic flux through the coil will decrease. It will create a change in magnetic flux and hence will induce an emf and a current. This current will create its own magnetic field and according to Lenz’s law this magnetic field will oppose the decrease in flux through the coil or we can say that the side of the coil towards the magnet will attain the south polarity.

Its mathematical formulation is such that:
$\in =-N\dfrac{\partial {{\phi }_{B}}}{\partial t}$
$\in $ is induced EMF
$\dfrac{\partial {{\phi }_{B}}}{\partial t}$ is change in flux
N is no. Of turns

Note: The induced magnetic field in the coil due to the electromagnetic induction will always oppose the change in the magnetic field or always oppose the motion of the magnet. We can find the direction of induced current by applying the right-hand thumb rule.