Question

State \[AAA\] - similarity criteria ?

Answer 1

Hint: In this problem, we will state the \[AAA\] - criteria for similarity of two triangles.
I.e. if three angles are equal in two triangles then, the two triangles are said to be similar.
Also if two corresponding angles of two triangles are equal then also the triangles are said to be similar.

Complete step-by-step answer:
Two triangle can be similar by following criteria:
AAA-Similarity ( also AA- Similarity)
SSS-Similarity
SAS- similarity
IF the corresponding sides of two similar triangles are equal then the triangle is said to be congruent triangles.
In congruent triangles, corresponding sides as well as corresponding angles are equal.
For example: If triangle \[\Delta ABC\] is similar to triangle \[\Delta DEF\], Then \[\angle A = \angle D\], \[\angle B = \angle E\] and \[\angle C = \angle F\]. Then the sides \[AB = DE\], \[BC = EF\] and \[AC = DF\] are equal.
\[AAA\] - Similarity: If all the corresponding angles of two triangles are equal , then the two triangles are said to be similar .
Let ABC and DEF be two triangle
We can write the two triangles are equal, \[ABC \equiv DEF\].
Let \[\angle A = \angle D\] , \[\angle B = \angle E\] and \[\angle C = \angle F\].

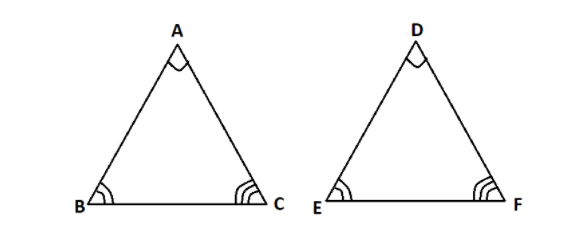
Since all the angles of the triangle \[\Delta ABC\] are equal to the corresponding angles of the triangle, \[\Delta DEF\] .
We say the triangles are similar.

Note: When two triangles are similar, then corresponding angles are equal. Corresponding sides are proportional.
For example: If triangle \[\Delta ABC\] is similar to triangle \[\Delta DEF\] , Then \[\angle A = \angle D\], \[\angle B = \angle E\] and \[\angle C = \angle F\], \[\dfrac{{AB}}{{DE}} = \dfrac{{BC}}{{EF}} = \dfrac{{AC}}{{DF}}\].
If two angles of a triangle are equal to the corresponding two angles of a triangle then the third angle is also equal to the corresponding third angle of the triangle. Thus we can say AA- Similarity.