Question

How many square meters of a canvas is required for a conical tent whose height is $3.5{\text{ m}}$ and the radius of the base is $12{\text{ m}}$.

Answer 1

Hint: We have to find the Lateral surface area of the canvas. Because when we build the conical tent we will require only the outer surface without the area of the base of the cone.
The lateral surface area of the cone is $\pi rl$

Complete Step-by-step Solution
Step 1: Finding the slant height of the cone.
Given,
Height of the cone $ = 3.5m$
Radius of the cone $ = 12m$

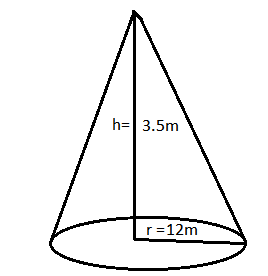
We know that :
${l^2} = {r^2} + {h^2}$ ….(i)
Here ,$l,r,h$ are slant height, radius, height respectively
Putting values of r and h in above equation.
${l^2} = {12^2} + {3.5^2}$
Squaring $12$ and$3.5$ we get,
${l^2} = 144 + 12.25$
Find square root of sum of r and h to obtain $l$
${l^2} = 156.25$
$l = 12.5m$
Step 2: Finding lateral surface area.
Lateral surface area$ = \pi rl$
Putting the values of r and l in above equation we get,
$
   = \pi \times 12.5 \times 12 \\
   = 150\pi \\
$
$150\pi $ is the lateral surface area of the canvas.

$\therefore $ The canvas is required for a conical tent is $150\pi$ sq.m

Note:
In this kind of problem, if radius and height are given then we have to find the slant height of the cone. To find the slant height we have used the Pythagoras theorem. One thing to be noted that we cannot use the Total surface area in this question because when we build a tent we do not use the canvas in the base of the tent but the total surface area includes the area of the base also and hence we have to use the lateral surface area of the cone.