Question

Solve this following inequality:
\[\sin x > -\dfrac{1}{2}\]
(a) \[2n\pi -\dfrac{\pi }{3} < x < 2n\pi +\dfrac{7\pi }{3};n\in \mathbb{Z}\]
(b) \[2n\pi -\dfrac{\pi }{5} < x < 2n\pi +\dfrac{6\pi }{5};n\in \mathbb{Z}\]
(c) \[2n\pi -\dfrac{\pi }{4} < x < 2n\pi +\dfrac{5\pi }{4};n\in \mathbb{Z}\]
(d) \[2n\pi -\dfrac{\pi }{6} < x < 2n\pi +\dfrac{7\pi }{6};n\in \mathbb{Z}\]

Answer 1

Hint: We solve this problem first by finding the exact solution then we can find the general solution.
We use the condition that the period for sine function is \[2\pi \] so that we find the solution in the domain \[\left[ -2\pi, 2\pi \right]\] of one complete curve that satisfies the given inequality then we can find the general solution.
For finding the exact solution we use graph theory that is if \[f\left( x \right) > g\left( x \right)\] then the solution is given by plotting the graph of \[y=f\left( x \right)\] and \[y=g\left( x \right)\] such that the domain above the intersection of both graphs will be the solution.
The general solution for a sine function of one complete curve such that the curve of \[y=\sin x\] is above the line \[y=-\dfrac{1}{2}\] is given by adding the \[2n\pi \]where \['n'\] is an integer to exact solution because the period of the sine function is \[2\pi \]

Complete step-by-step solution
We are given with the inequality that is
\[\sin x > -\dfrac{1}{2}\]
We know that the period of sine function is \[2\pi \] so that the exact solution will be in the domain \[\left[ -2\pi ,2\pi \right]\]
Let us use the graph theory to find the exact solution.
We know that if \[f\left( x \right) > g\left( x \right)\] then the solution is given by plotting the graph of \[y=f\left( x \right)\] and \[y=g\left( x \right)\] such that the domain above the intersection of both graphs will be the solution.
Now, let us plot the graphs \[y=\sin x\] and \[y=-\dfrac{1}{2}\] then we get

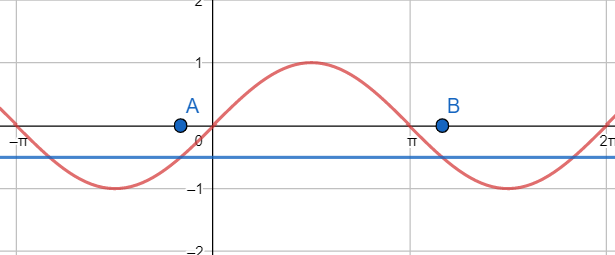
Here we can see that one complete curve of \[y=\sin x\] that is above the line \[y=-\dfrac{1}{2}\] is located between that points A and B where the co – ordinates of points are \[A\left( \dfrac{-\pi }{6},\dfrac{-1}{2} \right),B\left( \dfrac{7\pi }{6},\dfrac{-1}{2} \right)\]
So, we can say that the exact solution lies between these points.
So, by converting the above statement into mathematical inequality we get
\[\Rightarrow \dfrac{-\pi }{6} < x < \dfrac{7\pi }{6}\]
We know that the general solution of sine function is given by adding the \[2n\pi \]where \['n'\] is an integer to exact solution because the period of the sine function is \[2\pi \]
So, by adding the \[2n\pi \] in above equation we get
\[\Rightarrow 2n\pi -\dfrac{\pi }{6} < x < 2n\pi +\dfrac{7\pi }{6};n\in \mathbb{Z}\]
So, option (d) is the correct answer.

Note: We can find the exact solution without using the graph theory.
We are given the inequality that is
\[\sin x > -\dfrac{1}{2}\]
We know that the sine function is negative in the third and fourth quadrants.
So, we can take one value in this and one value in the fourth quadrant such that \[\sin x=-\dfrac{1}{2}\] and then we can change it into inequality by taking the value of \['x'\] between those two values.
We know that if \[\sin x=-\dfrac{1}{2}\] then \[x=\dfrac{-\pi }{6}\] is solution in fourth quadrant and \[x=\dfrac{7\pi }{6}\] in third quadrant.
So, we can take the inequality as
\[\Rightarrow \dfrac{-\pi }{6} < x < \dfrac{7\pi }{6}\]
So, by adding the \[2n\pi \] in the above equation we get
\[\Rightarrow 2n\pi -\dfrac{\pi }{6} < x < 2n\pi +\dfrac{7\pi }{6};n\in \mathbb{Z}\]
So, option (d) is the correct answer.