Question

How do you solve the triangle given $B={{75}^{\circ }}20',a=6.2,c=9.5$ ?

Answer 1

Hint: We solve problems on determining the triangle either by using the Law of cosines or by using the Law of Sines. As, we are given two sides of the triangle along with the angle between the two given sides. so, we use the Law of Cosines. Using the Law of cosines, we first find the other side of the triangle and putting the value of all the sides of the triangle in the other two laws of cosines we get the other angles of the triangle.

Complete step by step solution:
We can solve triangles using either the Law of cosines or the Law of Sines.
We are given that $B={{75}^{\circ }}20',a=6.2,c=9.5$
For this case we must use the Law of cosines as we are given two sides of the triangle along with the angle between the two given sides.
According to the Law of cosines ${{b}^{2}}={{a}^{2}}+{{c}^{2}}-2ac\cos B$
Substituting the values in the above formula we get
\[\Rightarrow {{b}^{2}}={{\left( 6.2 \right)}^{2}}+{{\left( 9.5 \right)}^{2}}-2\left( 6.2 \right)\left( 9.5 \right)\cos \left( {{75}^{\circ }}20' \right)\]
Further simplifying we get
\[\Rightarrow {{b}^{2}}=38.44+90.25-2\times \left( 58.9 \right)\times 0.253\]
\[\begin{align}
  & \Rightarrow {{b}^{2}}=98.8866 \\
 & \Rightarrow b=9.944 \\
\end{align}\]
Now, we have values of all the sides of the triangle. So, we use the other laws of cosines to get the values of other angles as shown below
${{a}^{2}}+{{b}^{2}}-2ab\cos C={{c}^{2}}$
Substituting the values in the above formula we get
$\Rightarrow {{\left( 6.2 \right)}^{2}}+{{\left( 9.944 \right)}^{2}}-2\left( 6.2 \right)\left( 9.944 \right)\cos C={{\left( 9.5 \right)}^{2}}$
Simplifying the above equation, we get
$\Rightarrow \cos C=\dfrac{{{\left( 6.2 \right)}^{2}}+{{\left( 9.944 \right)}^{2}}-{{\left( 9.5 \right)}^{2}}}{2\left( 6.2 \right)\left( 9.944 \right)}$
Taking cos inverse on both the sides of the above equation we get
$\begin{align}
  & \Rightarrow C={{\cos }^{-1}}\left( \dfrac{47.073}{123.3056} \right) \\
 & \Rightarrow C={{67.557}^{\circ }} \\
\end{align}$
We know that the summation of all the internal angles of a triangle is ${{180}^{\circ }}$ .
Hence, we subtract the summation of the two angles from ${{180}^{\circ }}$ which gives us the value of the other angle $A$ .
Therefore, $A={{180}^{\circ }}-\left( B+C \right)$
Putting the values in above equation we get
$A={{180}^{\circ }}-\left( {{75}^{\circ }}20'+{{67.557}^{\circ }} \right)$
Further simplifying we get
$\begin{align}
  & \Rightarrow A={{180}^{\circ }}-\left( {{142.89}^{\circ }} \right) \\
 & \Rightarrow A={{37.11}^{\circ }} \\
\end{align}$
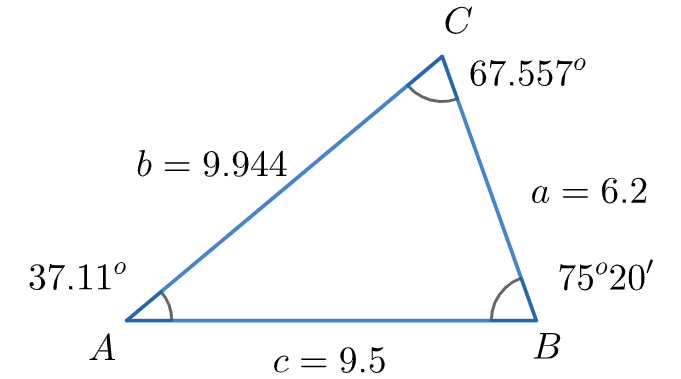
Therefore, in the triangle $A={{37.11}^{\circ }},B={{75}^{\circ }}20',C={{67.557}^{\circ }}$ and $a=6.2,b=9.944,c=9.5$ .

Note: While using the Laws of cosines we must be careful about the signs in the formula as students often get confused whether to put a negative or positive sign in front of $2ab$ and $2ac$ . Also, for a problem we must properly decide where to use the Laws of cosines and where to use the Laws of sines to get the correct solution.