Question

How do you solve the system\[\text{ }x+y-6=0\] and\[\text{ }x-y=0\] by graphing?

Answer 1

Hint: These types of problems are pretty straight forward and are very easy to solve. For solving these types of problems first and foremost we need to keep in mind the theory of linear equations. The given equations are of straight lines in the\[\text{ }x-y\] , \[2-D\] coordinate system. From the given two equations we can easily convert them into the “Intercept form” of the equations, whose general form is defined by:
\[\dfrac{x}{a}+\dfrac{y}{b}=1\]
Here, \[\text{ }a\]and\[\text{ }b\]are \[\text{ }x\] and\[\text{ }y\] intercepts respectively. The two equations, transformed into the standard form, makes the plotting of the graph very simple. After plotting the respective lines on the graph paper, their point of intersection is located. This point of intersection of the two straight lines is basically the solution of the system of linear equations.

Complete step by step solution:
Now, we start off with our solution and we write that, first the two equations are transformed into the "Intercept form", by dividing the first equation by \[6\] and the second equation by \[1\] . After transformation, we write the equations as:
\[\dfrac{x}{6}+\dfrac{y}{6}=1\text{ }\cdot \cdot \cdot \cdot \cdot \cdot \cdot \text{ eqn 1}\]
\[\dfrac{x}{1}-\dfrac{y}{1}=0\text{ }\cdot \cdot \cdot \cdot \cdot \cdot \cdot \text{ eqn 2}\]
We can further transform the second equation as\[\text{ }\dfrac{x}{1}+\dfrac{y}{-1}=0\] . After finding the intercepts of the two lines, we draw the first line with x and y intercepts as \[6\] each and the second line with x-intercept \[1\] and y-intercept as \[-1\] .
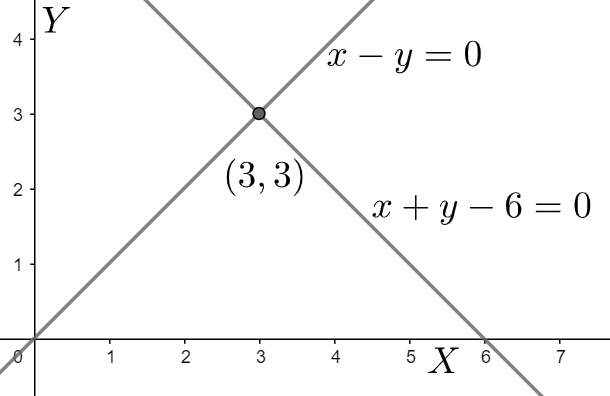
We then plot the graph on Geogebra, providing the “Intercept form” of the two linear equations. The point of intersection of the pair of straight lines is located on the graph and is noted down. It comes out to be \[\left( 3,3 \right)\] . The point of intersection of two straight lines is defined as the only point that lies on both the lines simultaneously. In other words, it is the only point that satisfies both the linear equations.

Note: For such problems we must also recapitulate graph theory a bit along with linear and simultaneous equations. We must be very careful while transforming the given equations into their standardized form, especially with the negative and positive signs. We can also do this problem in another form, i.e. using the slope-intercept form, but the above shown method is the most simplest and easy to understand. Proper scale must be used for accurate identification of the point of intersection.