Question

Solve the system of equations graphically
$\begin{align}
  & x-y=1 \\
 & 2x+y=8 \\
\end{align}$
Find the area bounded by these lines and y-axis

Answer 1

Hint: A line can be entirely determined by two points. So, to draw the line just take two points which satisfy the line equation and draw a line through those points in the graph. Plot these lines on the same graph and find the coordinates of their point of intersection. This will give the solution of the given system of equations , Now use intersection of two lines with the y-axis to find the base and height of the triangle to calculate the area.


Complete step-by-step answer:

For equation the equation $x-y=1$
When x = 0, we have $0-y=1$
Multiplying both sides by -1, we get
y =-1
When y = 0 we have $x-0=1$
Hence, we have x =1

We plot the points A $\left( 0,-1 \right)$ and B$\left( 1,0 \right)$ and draw a line through the points.

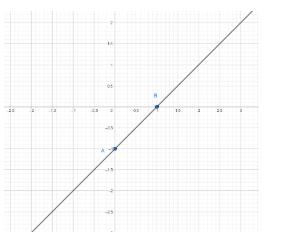
So, we have AB $\equiv x-y=1$
For equation $2x+y=8$
When x = 0, we have
$\begin{align}
  & 2\left( 0 \right)+y=8 \\
 & \Rightarrow y=8 \\
\end{align}$
Hence, we have y =8.
When y = 0, we have
$\begin{align}
  & 2x+0=8 \\
 & \Rightarrow 2x=8 \\
\end{align}$
Dividing both sides by 2, we get
x=4

We plot points C $\left( 0,8 \right)$ and D $\left( 4,0 \right)$ and draw line CD on the same graph.
So, CD $\equiv 2x+y=8$

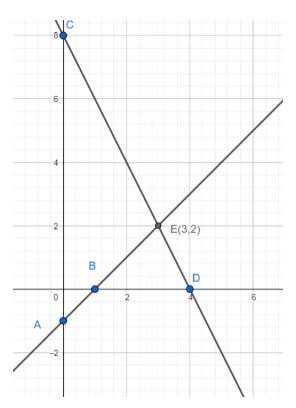
These lines intersect at point E.
We find the coordinates of point E as (3,2)
Since point E is satisfied by the equations of both the lines, E is the solution of the given system of equations.
Hence, we have x =3, and y = 2 is the solution of the given system of equations.
As is evident from the graph, area bounded by the lines and y-axis is the area of $\Delta \text{EAC}$, which is shown shaded in the following graph

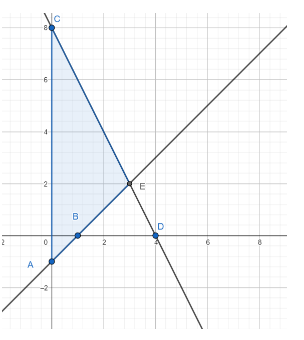
Here E (3,2),A (0,-1) and C (0,8).
We know that area of $\Delta =\dfrac{1}{2}base\times height$
Length of altitude from E to base AC = abscissa of E = 3
Length of BD = $8-\left( -1 \right)=8+1=9$
Using the formula of area of a triangle in $\Delta \text{EAC}$ we get
$\Delta \text{EAC=}\dfrac{1}{2}AC\times x-\text{coordinate of E=}\dfrac{1}{2}\times 9\times 3=\dfrac{27}{2}$ square units
Note: Equation of a line in intercept form is
$\dfrac{x}{a}+\dfrac{y}{b}=1$
This line passes through (a, 0) and (0, b)
So, we can directly find these points by writing the equation in intercept form.
e.g. $x-y=1$
$\Rightarrow \dfrac{x}{1}-\dfrac{y}{1}=1$
Hence a = 1 and b =-1
Hence the line passes through (1,0) and (0,-1)
Verification:
We can verify our solution by substituting the values of x and y and check if they satisfy the equation or not.
We have x =3 and y = 2
Hence, we have
$x-y=3-2=1$
Hence the first equation is satisfied.
Also, we have
$2x+y=2\left( 3 \right)+2=8$
Hence the second equation is also satisfied.
Hence our solution is verified to be correct.