Question

How do you solve the system of equations $2x+3y=105$ and $x+2y=65$?

Answer 1

Hint: In the problem we need to solve the two equations which are in two variables. For this type of equation, we will consider the coefficients of the variables in both equations. Now we will calculate the LCM of the coefficients of any one variable either $x$ or $y$. Now we will modify any one of the equations by multiplying with an appropriate constant so that the coefficients at least one variable must be equal. Now according to the sign of the coefficients we will add or subtract the both equations to get an equation in a single variable. Now we will simplify the obtained equation to get the value of one variable. After getting the value of one variable we will calculate the value of another variable by substituting the calculated value in any one of the given equations and simplify to get the result.

Complete step by step answer:
Given equations are $2x+3y=105$ and $x+2y=65$.
Coefficient of $x$ in the first equation is $2$.
Coefficient of $x$ in the second equation is $1$.
Coefficient of $y$ in the first equation is $3$.
Coefficient of $y$ in the second equation is $2$.
Considering the coefficients of variable $x$. We know that LCM of $2$, $1$ is $2\times 1=2$.
Multiplying the given second equation with $2$, then we will get
$\begin{align}
  & 2\left( x+2y \right)=2\times 65 \\
 & \Rightarrow 2x+4y=130....\left( \text{i} \right) \\
\end{align}$
Subtracting the equation $\left( \text{i} \right)$ from given first equation, then we will get
$2x+3y-\left( 2x+4y \right)=105-130$
Simplifying the above equation, then we will get
$\begin{align}
  & \Rightarrow 2x+3y-2x-4y=-25 \\
 & \Rightarrow -y=-25 \\
 & \Rightarrow y=25 \\
\end{align}$
Substituting this value in the given first equation, then we will get
$\begin{align}
  & \Rightarrow 2x+3\left( 25 \right)=105 \\
 & \Rightarrow 2x+75=105 \\
 & \Rightarrow 2x=30 \\
 & \Rightarrow x=15 \\
\end{align}$

Hence the solution for the given equations is $x=15$, $y=25$.

Note: We can also plot the graph of the given system of equation and calculate the solution from the intersection point of the system. Now the graph of the system of equations will be

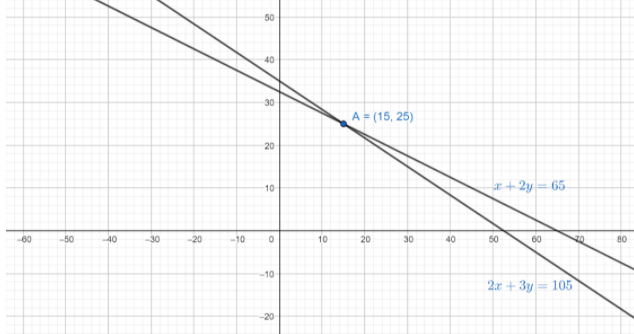
From the above graph also the solution of the given system will be $x=15$, $y=25$.