Question

Solve the following systems of linear equations graphically:
$\begin{align}
  & 2x-3y+13=0 \\
 & 3x-2y+12=0 \\
\end{align}$

Answer 1

Hint: Here, we will sketch the graph of both the given lines and then we will check that at which point they intersect each other. This point of intersection will give us the solution to the given system of linear equations.

Complete step-by-step answer:
The system of equations given to us here is:
$\begin{align}
  & 2x-3y+13=0..........\left( 1 \right) \\
 & 3x-2y+12=0.........\left( 2 \right) \\
\end{align}$
For the first line i.e. 2x-3y+13=0, we can give values of y corresponding to different values of x as follows:
When we take x = -2, we can write from equation (1):
$\begin{align}
  & 2\times \left( -2 \right)-3y+13=0 \\
 & \Rightarrow -4-3y+13=0 \\
 & \Rightarrow -3y=-9 \\
 & \Rightarrow y=3 \\
\end{align}$
When we take x=4, we have:
\[\begin{align}
  & 2\times 4-3y+13=0 \\
 & \Rightarrow -3y=-13-8 \\
 & \Rightarrow -3y=-21 \\
 & \Rightarrow y=7 \\
\end{align}\]
So, two points lying on the 1st line are (-2, 3) and (4, 7).
Similarly for the second line, i.e.3x-2y+12=0, we can give values of y corresponding to different values of x as follows:
When we take x = 2, we can write from equation (2):
$\begin{align}
  & 3\times 2-2y+12=0 \\
 & \Rightarrow 6-2y+12=0 \\
 & \Rightarrow 2y=18 \\
 & \Rightarrow y=9 \\
\end{align}$
When we take x = -2, we have:
$\begin{align}
  & 3\times \left( -2 \right)-2y+12=0 \\
 & \Rightarrow -6-2y+12=0 \\
 & \Rightarrow -2y=-6 \\
 & \Rightarrow y=3 \\
\end{align}$
 So, two points lying on the 2nd line are (2, 9) and (-2, 3).
So, the graph of the given lines can be made as:

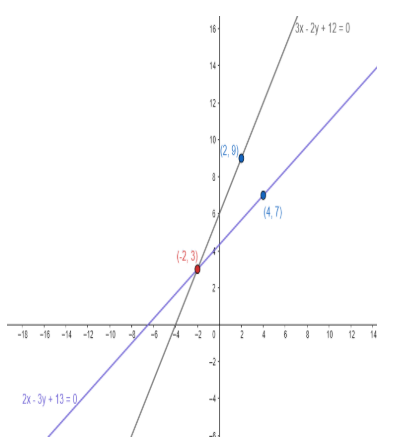
Now, the two lines intersect at the point (-2, 3).
Hence, x=-2 and y =3 is the solution of the given system of equations.

Note: Students should note here that we can take any value of x to get a corresponding value of y but for our convenience we should prefer to take simple values. The graph must be made properly. We can also cross- verify the answer by solving the equations algebraically.