Question

Solve the following LP problem using the simplex method, maximize $P=70x+50y$ subjected to $4x+3y\le 240,\text{ }2x+y\le 100,\text{ }x,y\ge 0$ .

Answer 1

Hint: Start by representing each condition given in the question in the form of mathematical equations and inequalities in the form of intercept forms of line. After you get all the equations, draw a representative graph and check at all the intersection of the lines, as according to LPP, the maximum and minimum values occur at the point of intersection of the lines.

Complete step-by-step answer:
To start with the solution, let us convert all the equations and inequality to intercept forms.:
$4x+3y\le 240$
$\Rightarrow \dfrac{x}{60}+\dfrac{y}{80}\le 1$
The next inequality is $2x+y\le 100$ . If we convert it to intercept form, we get
$\dfrac{x}{50}+\dfrac{y}{100}\le 1$
And two basic equations are $x\ge 0\text{ and y}\ge \text{0}$ .
So representing all the equations on graph, we get

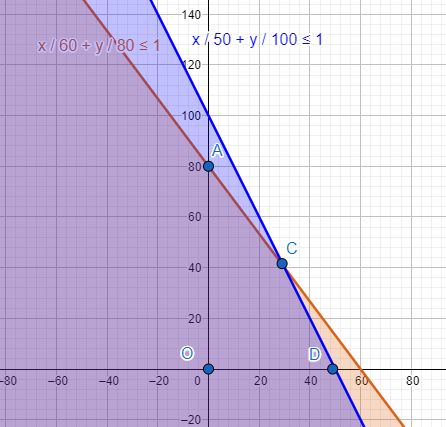
Therefore the objective equations are maximum and minimum at the boundary point of the feasible region AODC. Point A is (0,80), point D is (50,0) and O is (0,0). We can find point C by finding the intersection of the lines $4x+3y=240$ and $2x+y=100$ . Subtracting the equation of the second line multiplied by 2 from the equation of the first line. On doing so, we get
$\begin{align}
  & 4x+3y-4x-2y=240-200 \\
 & \Rightarrow y=40 \\
\end{align}$
Putting the value of y in equation of the first line, we get
$4x+3\times 40=240$
$\begin{align}
  & \Rightarrow 4x=120 \\
 & \Rightarrow x=30 \\
\end{align}$
So, point C is (30,40). Now we will check the value of $P=70x+50y$ at A, O, C, D.
At O(0,0), P is equal to 70x + 50y = 0
At D(50,0), P is equal to 70 $\times $ 50 + 500 = 3500
At C (30,40), P is equal to 70 $\times $ 30 + 50 $\times $ 40 = 4100
At A(0,80), the profit is equal to 70 $\times $ 0 + 50 $\times $ 80 = 4000
Therefore, the maximum possible value of P is 4100, and the value is possible when x=30 and y=40.

Note: Be sure that the graph is made properly with all the boundary points correctly plotted. Also, use different colours to plot different inequalities as this reduces the chance of making mistakes. If you can’t find the boundary points using the graph then solve all the inequalities taking two inequalities at a time to get the critical points as we did in the above question.