Question

Solve the following equations:
$x\left( a+x \right)=y\left( b+y \right)$ and $ax+by={{\left( x+y \right)}^{2}}$

Answer 1

Hint: Expand the first equation and keep the linear terms on LHS and quadratic terms on RHS. Now divide the second equation by the first equation and use ${{x}^{2}}-{{y}^{2}}=\left( x+y \right)\left( x-y \right)$. Use componendo-dividendo, i.e. if $\dfrac{a}{b}=\dfrac{c}{d}$, then $\dfrac{a+b}{a-b}=\dfrac{c+d}{c-d}$. Hence find the value of x in terms of y.

Complete step-by-step answer:
Substitute the value of x in the second equation and solve for y. Hence solve the given system of equations. Verify graphically.

We have $x\left( a+x \right)=y\left( b+y \right)$
Expanding, we get
$ax+{{x}^{2}}=by+{{y}^{2}}$
Adding $-{{x}^{2}}-by$ on both sides of the equation, we get
$ax-by={{y}^{2}}-{{x}^{2}}\text{ (i)}$
Also, we have
$ax+by={{\left( x+y \right)}^{2}}\text{ (ii)}$
Dividing equation (ii) by equation (i), we get
$\dfrac{ax+by}{ax-by}=\dfrac{{{\left( x+y \right)}^{2}}}{{{y}^{2}}-{{x}^{2}}}$
We know that ${{y}^{2}}-{{x}^{2}}=\left( y+x \right)\left( y-x \right)$
Hence, we have
$\dfrac{ax+by}{ax-by}=\dfrac{{{\left( x+y \right)}^{2}}}{\left( y+x \right)\left( y-x \right)}=\dfrac{y+x}{y-x}$
Applying componendo-dividendo, we get
$\begin{align}
  & \dfrac{ax+by+ax-by}{ax+by-\left( ax-by \right)}=\dfrac{y+x+y-x}{y+x-\left( y-x \right)} \\
 & \Rightarrow \dfrac{2ax}{2by}=\dfrac{2y}{2x} \\
\end{align}$
Hence, we have
$\dfrac{ax}{by}=\dfrac{y}{x}$
Cross-multiplying, we get
$ax\left( x \right)=by\left( y \right)\Rightarrow a{{x}^{2}}=b{{y}^{2}}$
Dividing both sides of the equation by a, we get
${{x}^{2}}=\dfrac{b}{a}{{y}^{2}}$
Hence, we have
$x=\pm \sqrt{\dfrac{b}{a}}y$
Hence, we have
$x=cy$, where $c=\pm \sqrt{\dfrac{b}{a}}$.
Substituting the value of x in equation (ii), we get
$a\left( cy \right)+by={{\left( cy+y \right)}^{2}}$
Hence, we have
$y\left( ac+b \right)={{y}^{2}}{{\left( 1+c \right)}^{2}}$
Subtracting y(ac+b) from both sides, we get
${{y}^{2}}{{\left( 1+c \right)}^{2}}-y\left( ac+b \right)=0$
Taking y common from the first two terms, we get
$y\left( y{{\left( 1+c \right)}^{2}}-\left( ac+b \right) \right)=0$
Using zero product property, we get
$y=0$ or $y{{\left( 1+c \right)}^{2}}-\left( ac+b \right)=0$
Solving $y{{\left( 1+c \right)}^{2}}-\left( ac+b \right)=0$:
Adding ac+b on both sides, we get
$y{{\left( 1+c \right)}^{2}}=ac+b$
Dividing by ${{\left( 1+c \right)}^{2}}$ on both sides, we get
$y=\dfrac{ac+b}{{{\left( 1+c \right)}^{2}}}$
Substituting the value of c, we get
$y=\dfrac{a\left( \pm \sqrt{\dfrac{b}{a}}+b \right)}{{{\left( 1\pm \sqrt{\dfrac{b}{a}} \right)}^{2}}}=\sqrt{\dfrac{b}{a}}\dfrac{\left( \sqrt{ab}\pm 1 \right)}{{{\left( \sqrt{a}\pm \sqrt{b} \right)}^{2}}}$
Taking +sign, we get
$y=\sqrt{\dfrac{b}{a}}\dfrac{\sqrt{ab}+1}{{{\left( \sqrt{a}+\sqrt{b} \right)}^{2}}}$ and hence $x=\sqrt{\dfrac{b}{a}}y=\dfrac{b}{a}\dfrac{\sqrt{ab}+1}{{{\left( \sqrt{a}+\sqrt{b} \right)}^{2}}}$
Taking -ve sign, we get
$y=\sqrt{\dfrac{b}{a}}\dfrac{\sqrt{ab}-1}{{{\left( \sqrt{a}-\sqrt{b} \right)}^{2}}}$ and hence we have $x=-\sqrt{\dfrac{b}{a}}y=-\dfrac{b}{a}\dfrac{\sqrt{ab}-1}{{{\left( \sqrt{a}-\sqrt{b} \right)}^{2}}}$
When y = 0, we have $x=0$
Hence, the solutions to the system are:
$\left( 0,0 \right),\left( \dfrac{b}{a}\dfrac{\sqrt{ab}+1}{{{\left( \sqrt{a}+\sqrt{b} \right)}^{2}}},\sqrt{\dfrac{b}{a}}\dfrac{\sqrt{ab}+1}{{{\left( \sqrt{a}+\sqrt{b} \right)}^{2}}} \right),\left( -\dfrac{b}{a}\dfrac{\sqrt{ab}-1}{{{\left( \sqrt{a}-\sqrt{b} \right)}^{2}}},\sqrt{\dfrac{b}{a}}\dfrac{\sqrt{ab}-1}{{{\left( \sqrt{a}-\sqrt{b} \right)}^{2}}} \right)$
Observe that when $a=b$, the third solution is not defined and hence only two solutions exist.
Also $a>0,b>0,a\ne b$ implies three solutions exist.
When $a<0$ or $b<0$ or $a=0$ only one solution exists

Note: Graph when $a\ne b$:

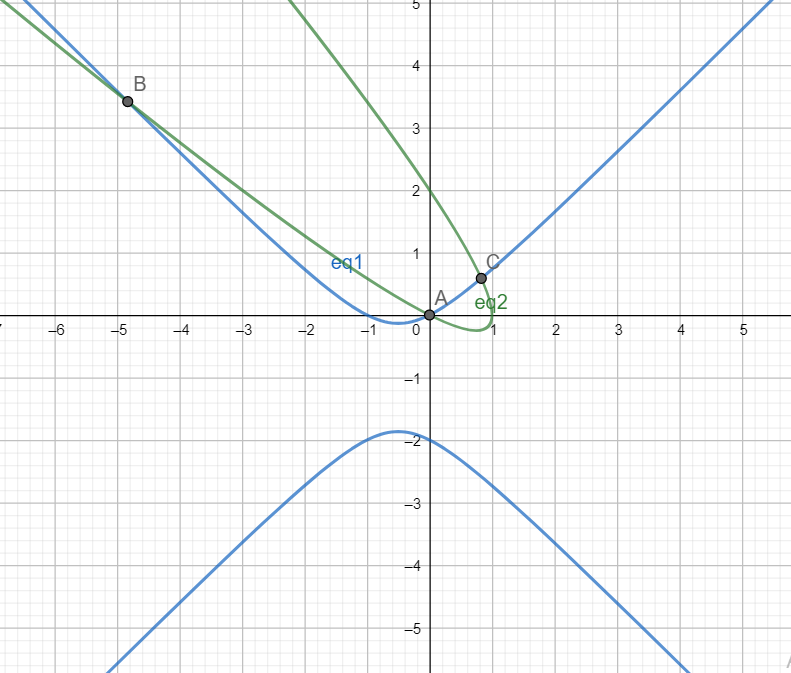
As is evident from the graph, three solutions A, B, C exist.
Graph when a=b:

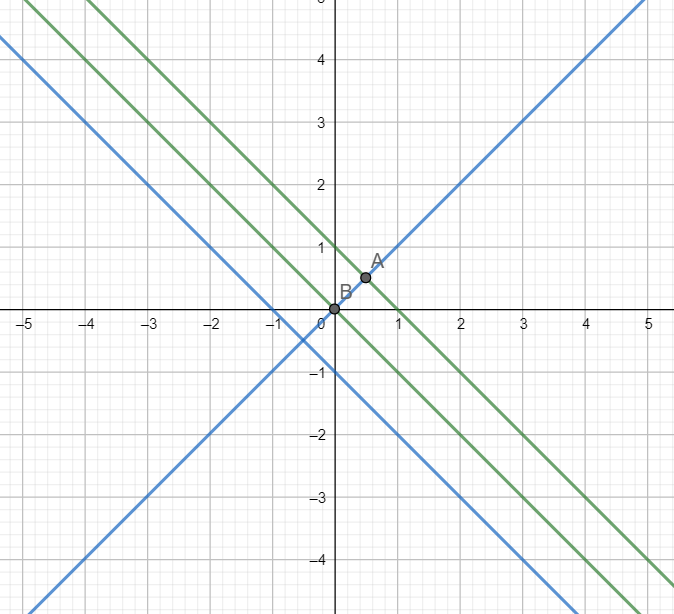
As is evident from the graph, two solutions A and B exist.