Question

How do you solve the \[\Delta HJK\] given h = 18, j = 10, k = 23?

Answer 1

Hint: In this problem, we have to solve the \[\Delta HJK\] from the given h = 18, j = 10, k = 23. We can use cosine rule from the Laws of cosine, to find H, J, K by substituting the values of h, j, k in the formula for the cosine rule. We can substitute the values for the area of the triangle to find its area.

Complete step by step solution:
We have to solve the, \[\Delta HJK\].
We are given h = 18, j = 10, k = 23.
We know that the cosine rule is,
\[\begin{align}
  & \cos A=\dfrac{{{b}^{2}}+{{c}^{2}}-{{a}^{2}}}{2bc} \\
 & \cos B=\dfrac{{{a}^{2}}+{{c}^{2}}-{{b}^{2}}}{2ac} \\
 & \cos C=\dfrac{{{b}^{2}}+{{a}^{2}}-{{c}^{2}}}{2ab} \\
\end{align}\]
We can now apply the cosine rule for H, J, K, we get

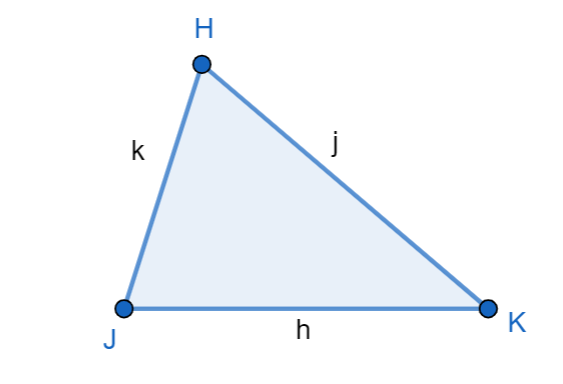
\[\Rightarrow \cos K=\dfrac{{{h}^{2}}+{{j}^{2}}-{{k}^{2}}}{2hj}\]
We can now substitute the value h = 18, j = 10, k = 23 in the above formula, we get
\[\Rightarrow \cos K=\dfrac{{{18}^{2}}+{{10}^{2}}-{{23}^{2}}}{2\times 18\times 10}\]
We can now simplify the above step, we get
\[\Rightarrow \cos K=\dfrac{{{18}^{2}}+{{10}^{2}}-{{23}^{2}}}{2\times 18\times 10}=-0.2917\]
We can now take cos inverse, we get
\[\begin{align}
  & \Rightarrow K={{\cos }^{-1}}\left( -0.2917 \right) \\
 & \Rightarrow K={{106.96}^{\circ }} \\
\end{align}\]
Similarly, we can find for H, we get
\[\begin{align}
  & \Rightarrow \cos H=\dfrac{{{23}^{2}}+{{10}^{2}}-{{18}^{2}}}{2\times 23\times 10}=0.663 \\
 & \Rightarrow H={{\cos }^{-1}}\left( 0.663 \right) \\
 & \Rightarrow H={{48.47}^{\circ }} \\
\end{align}\] \[\]
We can find J,
\[\begin{align}
  & \Rightarrow \cos J=\dfrac{{{23}^{2}}+{{18}^{2}}-{{10}^{2}}}{2\times 23\times 18}=0.9094 \\
 & \Rightarrow J={{\cos }^{-1}}\left( 0.9094 \right) \\
 & \Rightarrow J={{24.57}^{\circ }} \\
\end{align}\]
Now we have to solve \[\Delta HJK\].
Area of \[\Delta HJK\]\[=\dfrac{1}{2}hj\sin K\].
We can substitute the required values, we get
 Area of \[\Delta HJK\]\[=\dfrac{1}{2}\times 18\times 10\times \sin \left( {{106.96}^{\circ }} \right)\].
We can now simplify the above step, we get
Area of \[\Delta HJK\]\[=86.086\]square units.
Therefore, the Area of \[\Delta HJK\]\[=86.086\] square units.

Note: Students make mistakes while finding the value of H, J, K, by using the cosine rule. We can use a calculator to find the cos inverse values to get the value of angles. We should know that we can solve a triangle by finding the area of the triangle. We can use a calculator to find the trigonometric degree values.