Question

How do you solve \[\log x+\log \left( 5-x \right)=0\]?

Answer 1

Hint: Convert the R.H.S. of the given expression into logarithmic form by using the conversion: - \[0=\log 1\]. Now, in the L.H.S. use the sum to product rule of logarithm given as: - \[\log m+\log n=\log \left( mn \right)\] to simplify. In the next step form a quadratic equation by removing the logarithmic function. Solve this quadratic equation using the discriminant method to find the two values of x. Reject the value of x that is invalid using the information that “argument of the logarithmic function must be greater than 0”.

Complete step by step answer:
Here, we have been provided with the equation: - \[\log x+\log \left( 5-x \right)=0\] and we are asked to solve it. That means we need to find the value of x.
Now, since we have natural log on both the sides, i.e., log to the base 10, so we can write the given expression as: -
\[\Rightarrow \log x+\log \left( 5-x \right)=\log 1\left( \because \log 1=0 \right)\]
Applying the sum to product conversion formula of log given as: - \[\log m+\log n=\log \left( mn \right)\], we get,
\[\begin{align}
  & \Rightarrow \log \left( x\left( 5-x \right) \right)=\log 1 \\
 & \Rightarrow \log \left( 5x-{{x}^{2}} \right)=\log 1 \\
\end{align}\]
Now, comparing the arguments of log on both the sides by removing the logarithmic function, we get,
\[\begin{align}
  & \Rightarrow 5x-{{x}^{2}}=1 \\
 & \Rightarrow {{x}^{2}}-5x+1=0 \\
\end{align}\]
Using the discriminant formula to determine the value of x, we get,
\[\Rightarrow x=\dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}\]
Here, a = coefficient of \[{{x}^{2}}=1\]
b = coefficient of x = -5
c = constant term = 1
So, substituting the values of a, b and c in the above-mentioned discriminant formula, we get,
\[\begin{align}
  & \Rightarrow x=\dfrac{-\left( -5 \right)\pm \sqrt{{{\left( -5 \right)}^{2}}-4\times 1\times 1}}{2\times 1} \\
 & \Rightarrow x=\dfrac{5\pm \sqrt{21}}{2} \\
\end{align}\]
\[\Rightarrow x=\dfrac{5-\sqrt{21}}{2}\] or \[x=\dfrac{5+\sqrt{21}}{2}\].
Here, we have obtained two values of x. Now, let us check if any of the two values is invalid or not.
We know that a logarithmic function is defined only when its argument is greater than 0 and base is also greater than 0 but unequal to 1. In the above question we have log to the base 10 which is greater than 0 and also unequal to 1. So, base is defined. Now, let us define the argument. In the L.H.S. we have x and 5 – x as the arguments. So, we must have,
(i) \[x>0\Rightarrow x\in \left( 0,\infty \right)\]
(ii) \[5-x>0\Rightarrow x\in \left( -\infty ,5 \right)\]
Consider the intersection of the two sets of values of x obtained. So, we have,

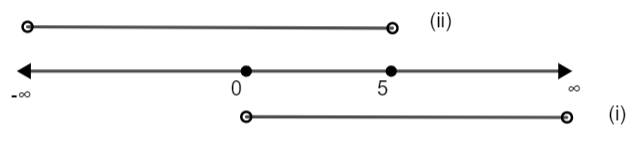
Therefore, \[x\in \left( 0,5 \right)\] is the final condition.
Clearly, we can see that both the values of x obtained by the discriminant method lies in the interval (0, 5).
Hence, \[x=\dfrac{5\pm \sqrt{21}}{2}\] is our answer.

Note: One may note that we cannot remove the logarithmic function directly from the initial expression: - \[\log x+\log \left( 5-x \right)=0\] as it will be a wrong approach. First, we need to convert the two logarithmic terms in the L.H.S. into a single logarithmic term by using the sum to product rule and then only we can remove the function. Remember that we do not just have to calculate the value of x but we must check if it satisfies the domain or not. We must reject the invalid value as it makes the function undefined.