Question

How do you solve $\ln \left( x \right) + {e^x} = 0$?

Answer 1

Hint: We are given an expression. We have to simplify the expression. First, move one term to the right hand side of the expression. Then, plot the graph of expression at the left hand side and right hand side of the expression. Then, find the intersection point of both the curves which is the required solution.

Complete step by step solution:
Given expression is $\ln \left( x \right) + {e^x} = 0$.

Now, subtract ${e^x}$ from both sides.

$ \Rightarrow \ln \left( x \right) + {e^x} - {e^x} = 0 - {e^x}$

On combining like terms, we get:

$ \Rightarrow \ln \left( x \right) = - {e^x}$

Now, plot the curve of the $\ln \left( x \right)$ and $ - {e^x}$ into the same set of axes.

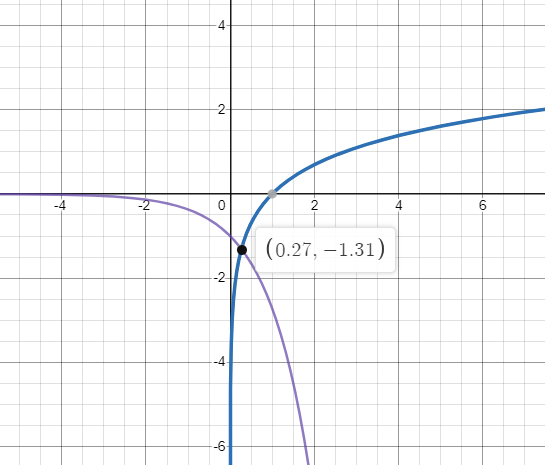
From the graph it is observed the curve of both functions intersect at point $\left( {0.27, - 1.31} \right)$.


he solution of the equation $\ln \left( x \right) + {e^x} = 0$ is $x = 0.27$

Note: The students please note the question can be solved by Newton’s formula which is described here.
Newton’s formula is used to approximate the roots of the equation. It states that ${x_{n + 1}} = {x_n} - \dfrac{{f\left( {{x_n}} \right)}}{{f'\left( {{x_n}} \right)}}$
Now, we will determine the starting value of x, to determine the approximate solution of the function.
Let the function be $y = \ln x + {e^x}f\left( x \right)$

Now, we will find the derivative of the function.

  $ \Rightarrow \dfrac{{dy}}{{dx}} = \dfrac{d}{{dx}}\left( {\ln x + {e^x}f\left( x \right)} \right)$

$ \Rightarrow f'\left( x \right) = \dfrac{1}{x} + {e^x}$

Now, we will use the initial approximation of $x = 1$

$ \Rightarrow f\left( {{x_1}} \right) = \ln \left( 1 \right) + {e^1}$

Substitute the value of $\ln \left( 1 \right) = 0$ to the expression.

$ \Rightarrow f\left( {{x_1}} \right) = 0 + e = e$

Now, we will find the value of $f'\left( 1 \right)$ by substituting $x = 1$ into the function.

$ \Rightarrow f'\left( {{x_1}} \right) = \dfrac{1}{1} + {e^1}$

On simplifying the expression further, we get:

$ \Rightarrow f'\left( {{x_1}} \right) = 1 + e$

Now, we will find the first approximation using ${x_{n + 1}} = {x_n} - \dfrac{{f\left( {{x_n}} \right)}}{{f'\left( {{x_n}} \right)}}$

$ \Rightarrow {x_{1 + 1}} = {x_1} - \dfrac{{f\left( {{x_1}} \right)}}{{f'\left( {{x_1}} \right)}}$

Substitute the values of $f\left( {{x_1}} \right)$ and $f'\left( {{x_1}} \right)$ into the expression.

$ \Rightarrow {x_2} = 1 - \dfrac{e}{{1 + e}}$

Now, substitute $e = 2.7$ into the expression.


$ \Rightarrow {x_2} = 1 - \dfrac{{2.7}}{{1 + 2.7}}$

On simplifying the expression, we get:

$ \Rightarrow {x_2} = 1 - \dfrac{{2.7}}{{3.7}}$

$ \Rightarrow {x_2} = \dfrac{1}{{3.7}}$

On simplifying the expression further, we get:

$ \Rightarrow {x_2} \approx 0.27$

Therefore, the answer is same using this method also that is $x = 0.27$