
How do you solve $\left| {\dfrac{5}{{2x - 1}}} \right| \geqslant \left| {\dfrac{1}{{x - 2}}} \right|?$
Answer
541.5k+ views
Hint: The given inequality is in modulus function, it can be solved by taking different cases for domain of the given modulus functions so that we can open it with positive or negative sign accordingly, then solve for all the cases and finally take the union of all results.
Modulus function can be understood as following:
$\left| x \right| = \left\{ {\begin{array}{*{20}{c}}
x&{{\text{if}}\;x > 0} \\
{ - x}&{{\text{if}}\,x < 0}
\end{array}} \right\}$
Complete step by step answer:
To solve the inequation $\left| {\dfrac{5}{{2x - 1}}} \right| \geqslant \left| {\dfrac{1}{{x - 2}}} \right|$ we have to take different cases for domain of the function
To get the cases we will compare variables separately with zero,
$
\Rightarrow 2x - 1 = 0\;{\text{and}}\;x - 2 = 0 \\
\Rightarrow x = \dfrac{1}{2}\;{\text{and}}\;x = 2 \\
$
$x = \dfrac{1}{2}\;{\text{and}}\;x = 2$ Can’t be in domain because inequality is undefined for them, i.e. $\dfrac{1}{0}$
There are three cases forming
Case I:
When $x \in \left( { - \infty ,\;\dfrac{1}{2}} \right)$, where
$
\left| {2x - 1} \right| = - (2x - 1) = - 2x + 1 = 1 - 2x \\
\left| {x - 2} \right| = - (x - 2) = - x + 2 = 2 - x \\
$
$\therefore $ inequality will be written as
$
\Rightarrow \left| {\dfrac{5}{{2x - 1}}} \right| \geqslant \left| {\dfrac{1}{{x - 2}}} \right| \\
\Rightarrow \dfrac{5}{{1 - 2x}} \geqslant \dfrac{1}{{2 - x}} \\
\Rightarrow \dfrac{5}{{1 - 2x}} \geqslant \dfrac{1}{{2 - x}} \\
\Rightarrow \dfrac{5}{{1 - 2x}} - \dfrac{1}{{2 - x}} \geqslant 0 \\
\Rightarrow \dfrac{{5(2 - x) - 1(1 - 2x)}}{{(1 - 2x)(2 - x)}} \geqslant 0 \\
\Rightarrow \dfrac{{10 - 5x - 1 + 2x}}{{(1 - 2x)(2 - x)}} \geqslant 0 \\
\Rightarrow \dfrac{{9 - 3x}}{{(1 - 2x)(2 - x)}} \geqslant 0 \\
\Rightarrow \dfrac{{3(3 - x)}}{{(1 - 2x)(2 - x)}} \geqslant 0 \\
\Rightarrow \dfrac{{(3 - x)}}{{(1 - 2x)(2 - x)}} \geqslant 0 \\
$
Now, we will compare variable terms with zero to find values for $x$, then plot them on number line to check which interval is satisfying the condition.
$
\Rightarrow 3 - x = 0,\;1 - 2x = 0\;{\text{and}}\;2 - x = 0 \\
\Rightarrow x = 3,\;x = \dfrac{1}{2}\;{\text{and}}\;x = 2 \\
$
Plotting them on a number line,
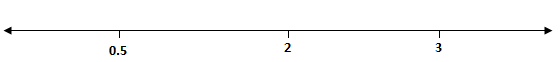
Take value of $x$ from any interval and check which sign it is giving $( + )\;{\text{or}}\;( - )$, then put the sign on that interval and alternative sign on its alternative intervals,
Checking for $x = 0\;which\; \in \left( { - \infty ,\;\dfrac{1}{2}} \right)$
$
\Rightarrow \dfrac{{(3 - x)}}{{(1 - 2x)(2 - x)}} \geqslant 0 \\
\Rightarrow \dfrac{{(3 - 0)}}{{(1 - 2 \times 0)(2 - 0)}} \geqslant 0 \\
\Rightarrow \dfrac{{(3)}}{{(1)(2)}} \geqslant 0 \\
\Rightarrow \dfrac{3}{2} \geqslant 0 \\
$
$\therefore $ putting the $( + )\;{\text{and}}\;( - )$ signs alternatively
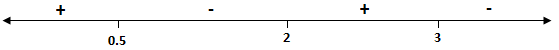
\[ \Rightarrow x \in \left( { - \infty ,\;\dfrac{1}{2}} \right) \cup (2,\;3] \cap \left( { - \infty ,\;\dfrac{1}{2}} \right)\]
$\because $ case is $x \in \left( { - \infty ,\;\dfrac{1}{2}} \right)$
\[\therefore x \in \left( { - \infty ,\;\dfrac{1}{2}} \right)\] is the solution for this case
Case II:
$x \in \left( {\dfrac{1}{2},\;2} \right),$ then
$
\left| {2x - 1} \right| = (2x - 1) = 2x - 1 \\
\left| {x - 2} \right| = - (x - 2) = - x + 2 = 2 - x \\
$
$\therefore $ inequality will be written as
$
\Rightarrow \left| {\dfrac{5}{{2x - 1}}} \right| \geqslant \left| {\dfrac{1}{{x - 2}}} \right| \\
\Rightarrow \dfrac{5}{{2x - 1}} \geqslant \dfrac{1}{{2 - x}} \\
\Rightarrow \dfrac{5}{{2x - 1}} \geqslant \dfrac{1}{{2 - x}} \\
\Rightarrow \dfrac{5}{{2x - 1}} + \dfrac{1}{{x - 2}} \geqslant 0 \\
\Rightarrow \dfrac{{5(x - 2) + 1(2x - 1)}}{{(2x - 1)(x - 2)}} \geqslant 0 \\
\Rightarrow \dfrac{{5x - 10 + 2x - 1}}{{(2x - 1)(x - 2)}} \geqslant 0 \\
\Rightarrow \dfrac{{(7x - 11)}}{{(2x - 1)(x - 2)}} \geqslant 0 \\
$
Again doing similar steps as case I,
$
\Rightarrow 7x - 11 = 0,\;2x - 1 = 0\;{\text{and}}\;x - 2 = 0 \\
\Rightarrow x = \dfrac{{11}}{7},\;x = \dfrac{1}{2}\;{\text{and}}\;x = 2 \\
$
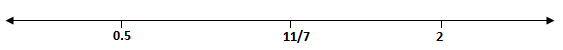
Checking for $x = 0\;which\; \in \left( { - \infty ,\;\dfrac{1}{2}} \right)$
\[
\Rightarrow \dfrac{{(7x - 11)}}{{(2x - 1)(x - 2)}} \geqslant 0 \\
\Rightarrow \dfrac{{(7 \times 0 - 11)}}{{(2 \times 0 - 1)(0 - 2)}} \geqslant 0 \\
\Rightarrow \dfrac{{( - 11)}}{{( - 1)( - 2)}} \geqslant 0 \\
\Rightarrow \dfrac{{ - 11}}{2} \geqslant 0 \\
\]
This is not true, so putting the signs accordingly
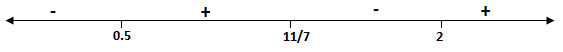
\[ \Rightarrow x \in \left( {\dfrac{1}{2},\;\dfrac{{11}}{7}} \right] \cup (2,\;\infty ) \cap \left( {\dfrac{1}{2},\;2} \right)\]
$\because $ case is $x \in \left( {\dfrac{1}{2},\;2} \right)$
$\therefore x \in \left( {\dfrac{1}{2},\;\dfrac{{11}}{7}} \right]$ is the solution for this case
Case III:
\[x \in \left( {2,\;\infty } \right),\] then
$
\left| {2x - 1} \right| = (2x - 1) = 2x - 1 \\
\left| {x - 2} \right| = (x - 2) = x - 2 \\
$
$\therefore $ inequality will be written as
$
\Rightarrow \left| {\dfrac{5}{{2x - 1}}} \right| \geqslant \left| {\dfrac{1}{{x - 2}}} \right| \\
\Rightarrow \dfrac{5}{{2x - 1}} \geqslant \dfrac{1}{{x - 2}} \\
\Rightarrow \dfrac{5}{{2x - 1}} \geqslant \dfrac{1}{{x - 2}} \\
\Rightarrow \dfrac{5}{{2x - 1}} - \dfrac{1}{{x - 2}} \geqslant 0 \\
\Rightarrow \dfrac{{5(x - 2) - 1(2x - 1)}}{{(2x - 1)(x - 2)}} \geqslant 0 \\
\Rightarrow \dfrac{{5x - 10 - 2x + 1}}{{(2x - 1)(x - 2)}} \geqslant 0 \\
\Rightarrow \dfrac{{(3x - 9)}}{{(2x - 1)(x - 2)}} \geqslant 0 \\
\Rightarrow \dfrac{{3(x - 3)}}{{(2x - 1)(x - 2)}} \geqslant 0 \\
\Rightarrow \dfrac{{(x - 3)}}{{(2x - 1)(x - 2)}} \geqslant 0 \\
$
Doing similar steps,
$
\Rightarrow x - 3 = 0,\;2x - 1 = 0\;{\text{and}}\;x - 2 = 0 \\
\Rightarrow x = 3,\;x = \dfrac{1}{2}\;{\text{and}}\;x = 2 \\
$
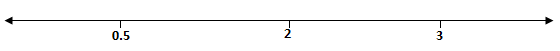
Checking for $x = 0\;which\; \in \left( { - \infty ,\;\dfrac{1}{2}} \right)$
\[
\Rightarrow \dfrac{{(x - 3)}}{{(2x - 1)(x - 2)}} \geqslant 0 \\
\Rightarrow \dfrac{{(0 - 3)}}{{(2 \times 0 - 1)(0 - 2)}} \geqslant 0 \\
\Rightarrow \dfrac{{( - 3)}}{{( - 1)( - 2)}} \geqslant 0 \\
\Rightarrow \dfrac{{ - 3}}{2} \geqslant 0 \\
\]
This is not true, so putting the signs accordingly
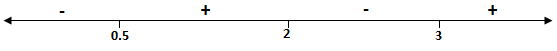
\[ \Rightarrow x \in \left( {\dfrac{1}{2},\;2} \right) \cup [3,\;\infty ) \cap \left( {2,\;\infty } \right)\]
$\because $ case is $x \in \left( {2,\;\infty } \right)$
$\therefore x \in [3,\;\infty )$ is the solution for this case
For final solution taking union of all results
\[ \Rightarrow x \in \left( { - \infty ,\;\dfrac{1}{2}} \right) \cup \left( {\dfrac{1}{2},\;\dfrac{{11}}{7}} \right] \cup [3,\;\infty )\] is the final solution
Note: Square brackets stand for the including the number and parentheses stand for excluding the number. One can put alternative signs on the number line only when the degree of all the terms is $1$. We have excluded $ - \infty \;{\text{and}}\;\infty $ because they doesn’t exist physically.
Modulus function can be understood as following:
$\left| x \right| = \left\{ {\begin{array}{*{20}{c}}
x&{{\text{if}}\;x > 0} \\
{ - x}&{{\text{if}}\,x < 0}
\end{array}} \right\}$
Complete step by step answer:
To solve the inequation $\left| {\dfrac{5}{{2x - 1}}} \right| \geqslant \left| {\dfrac{1}{{x - 2}}} \right|$ we have to take different cases for domain of the function
To get the cases we will compare variables separately with zero,
$
\Rightarrow 2x - 1 = 0\;{\text{and}}\;x - 2 = 0 \\
\Rightarrow x = \dfrac{1}{2}\;{\text{and}}\;x = 2 \\
$
$x = \dfrac{1}{2}\;{\text{and}}\;x = 2$ Can’t be in domain because inequality is undefined for them, i.e. $\dfrac{1}{0}$
There are three cases forming
Case I:
When $x \in \left( { - \infty ,\;\dfrac{1}{2}} \right)$, where
$
\left| {2x - 1} \right| = - (2x - 1) = - 2x + 1 = 1 - 2x \\
\left| {x - 2} \right| = - (x - 2) = - x + 2 = 2 - x \\
$
$\therefore $ inequality will be written as
$
\Rightarrow \left| {\dfrac{5}{{2x - 1}}} \right| \geqslant \left| {\dfrac{1}{{x - 2}}} \right| \\
\Rightarrow \dfrac{5}{{1 - 2x}} \geqslant \dfrac{1}{{2 - x}} \\
\Rightarrow \dfrac{5}{{1 - 2x}} \geqslant \dfrac{1}{{2 - x}} \\
\Rightarrow \dfrac{5}{{1 - 2x}} - \dfrac{1}{{2 - x}} \geqslant 0 \\
\Rightarrow \dfrac{{5(2 - x) - 1(1 - 2x)}}{{(1 - 2x)(2 - x)}} \geqslant 0 \\
\Rightarrow \dfrac{{10 - 5x - 1 + 2x}}{{(1 - 2x)(2 - x)}} \geqslant 0 \\
\Rightarrow \dfrac{{9 - 3x}}{{(1 - 2x)(2 - x)}} \geqslant 0 \\
\Rightarrow \dfrac{{3(3 - x)}}{{(1 - 2x)(2 - x)}} \geqslant 0 \\
\Rightarrow \dfrac{{(3 - x)}}{{(1 - 2x)(2 - x)}} \geqslant 0 \\
$
Now, we will compare variable terms with zero to find values for $x$, then plot them on number line to check which interval is satisfying the condition.
$
\Rightarrow 3 - x = 0,\;1 - 2x = 0\;{\text{and}}\;2 - x = 0 \\
\Rightarrow x = 3,\;x = \dfrac{1}{2}\;{\text{and}}\;x = 2 \\
$
Plotting them on a number line,
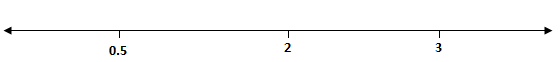
Take value of $x$ from any interval and check which sign it is giving $( + )\;{\text{or}}\;( - )$, then put the sign on that interval and alternative sign on its alternative intervals,
Checking for $x = 0\;which\; \in \left( { - \infty ,\;\dfrac{1}{2}} \right)$
$
\Rightarrow \dfrac{{(3 - x)}}{{(1 - 2x)(2 - x)}} \geqslant 0 \\
\Rightarrow \dfrac{{(3 - 0)}}{{(1 - 2 \times 0)(2 - 0)}} \geqslant 0 \\
\Rightarrow \dfrac{{(3)}}{{(1)(2)}} \geqslant 0 \\
\Rightarrow \dfrac{3}{2} \geqslant 0 \\
$
$\therefore $ putting the $( + )\;{\text{and}}\;( - )$ signs alternatively
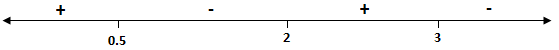
\[ \Rightarrow x \in \left( { - \infty ,\;\dfrac{1}{2}} \right) \cup (2,\;3] \cap \left( { - \infty ,\;\dfrac{1}{2}} \right)\]
$\because $ case is $x \in \left( { - \infty ,\;\dfrac{1}{2}} \right)$
\[\therefore x \in \left( { - \infty ,\;\dfrac{1}{2}} \right)\] is the solution for this case
Case II:
$x \in \left( {\dfrac{1}{2},\;2} \right),$ then
$
\left| {2x - 1} \right| = (2x - 1) = 2x - 1 \\
\left| {x - 2} \right| = - (x - 2) = - x + 2 = 2 - x \\
$
$\therefore $ inequality will be written as
$
\Rightarrow \left| {\dfrac{5}{{2x - 1}}} \right| \geqslant \left| {\dfrac{1}{{x - 2}}} \right| \\
\Rightarrow \dfrac{5}{{2x - 1}} \geqslant \dfrac{1}{{2 - x}} \\
\Rightarrow \dfrac{5}{{2x - 1}} \geqslant \dfrac{1}{{2 - x}} \\
\Rightarrow \dfrac{5}{{2x - 1}} + \dfrac{1}{{x - 2}} \geqslant 0 \\
\Rightarrow \dfrac{{5(x - 2) + 1(2x - 1)}}{{(2x - 1)(x - 2)}} \geqslant 0 \\
\Rightarrow \dfrac{{5x - 10 + 2x - 1}}{{(2x - 1)(x - 2)}} \geqslant 0 \\
\Rightarrow \dfrac{{(7x - 11)}}{{(2x - 1)(x - 2)}} \geqslant 0 \\
$
Again doing similar steps as case I,
$
\Rightarrow 7x - 11 = 0,\;2x - 1 = 0\;{\text{and}}\;x - 2 = 0 \\
\Rightarrow x = \dfrac{{11}}{7},\;x = \dfrac{1}{2}\;{\text{and}}\;x = 2 \\
$
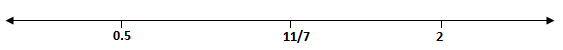
Checking for $x = 0\;which\; \in \left( { - \infty ,\;\dfrac{1}{2}} \right)$
\[
\Rightarrow \dfrac{{(7x - 11)}}{{(2x - 1)(x - 2)}} \geqslant 0 \\
\Rightarrow \dfrac{{(7 \times 0 - 11)}}{{(2 \times 0 - 1)(0 - 2)}} \geqslant 0 \\
\Rightarrow \dfrac{{( - 11)}}{{( - 1)( - 2)}} \geqslant 0 \\
\Rightarrow \dfrac{{ - 11}}{2} \geqslant 0 \\
\]
This is not true, so putting the signs accordingly
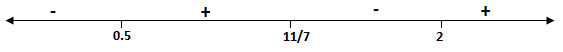
\[ \Rightarrow x \in \left( {\dfrac{1}{2},\;\dfrac{{11}}{7}} \right] \cup (2,\;\infty ) \cap \left( {\dfrac{1}{2},\;2} \right)\]
$\because $ case is $x \in \left( {\dfrac{1}{2},\;2} \right)$
$\therefore x \in \left( {\dfrac{1}{2},\;\dfrac{{11}}{7}} \right]$ is the solution for this case
Case III:
\[x \in \left( {2,\;\infty } \right),\] then
$
\left| {2x - 1} \right| = (2x - 1) = 2x - 1 \\
\left| {x - 2} \right| = (x - 2) = x - 2 \\
$
$\therefore $ inequality will be written as
$
\Rightarrow \left| {\dfrac{5}{{2x - 1}}} \right| \geqslant \left| {\dfrac{1}{{x - 2}}} \right| \\
\Rightarrow \dfrac{5}{{2x - 1}} \geqslant \dfrac{1}{{x - 2}} \\
\Rightarrow \dfrac{5}{{2x - 1}} \geqslant \dfrac{1}{{x - 2}} \\
\Rightarrow \dfrac{5}{{2x - 1}} - \dfrac{1}{{x - 2}} \geqslant 0 \\
\Rightarrow \dfrac{{5(x - 2) - 1(2x - 1)}}{{(2x - 1)(x - 2)}} \geqslant 0 \\
\Rightarrow \dfrac{{5x - 10 - 2x + 1}}{{(2x - 1)(x - 2)}} \geqslant 0 \\
\Rightarrow \dfrac{{(3x - 9)}}{{(2x - 1)(x - 2)}} \geqslant 0 \\
\Rightarrow \dfrac{{3(x - 3)}}{{(2x - 1)(x - 2)}} \geqslant 0 \\
\Rightarrow \dfrac{{(x - 3)}}{{(2x - 1)(x - 2)}} \geqslant 0 \\
$
Doing similar steps,
$
\Rightarrow x - 3 = 0,\;2x - 1 = 0\;{\text{and}}\;x - 2 = 0 \\
\Rightarrow x = 3,\;x = \dfrac{1}{2}\;{\text{and}}\;x = 2 \\
$
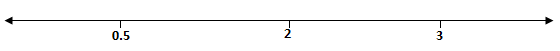
Checking for $x = 0\;which\; \in \left( { - \infty ,\;\dfrac{1}{2}} \right)$
\[
\Rightarrow \dfrac{{(x - 3)}}{{(2x - 1)(x - 2)}} \geqslant 0 \\
\Rightarrow \dfrac{{(0 - 3)}}{{(2 \times 0 - 1)(0 - 2)}} \geqslant 0 \\
\Rightarrow \dfrac{{( - 3)}}{{( - 1)( - 2)}} \geqslant 0 \\
\Rightarrow \dfrac{{ - 3}}{2} \geqslant 0 \\
\]
This is not true, so putting the signs accordingly
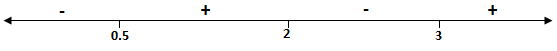
\[ \Rightarrow x \in \left( {\dfrac{1}{2},\;2} \right) \cup [3,\;\infty ) \cap \left( {2,\;\infty } \right)\]
$\because $ case is $x \in \left( {2,\;\infty } \right)$
$\therefore x \in [3,\;\infty )$ is the solution for this case
For final solution taking union of all results
\[ \Rightarrow x \in \left( { - \infty ,\;\dfrac{1}{2}} \right) \cup \left( {\dfrac{1}{2},\;\dfrac{{11}}{7}} \right] \cup [3,\;\infty )\] is the final solution
Note: Square brackets stand for the including the number and parentheses stand for excluding the number. One can put alternative signs on the number line only when the degree of all the terms is $1$. We have excluded $ - \infty \;{\text{and}}\;\infty $ because they doesn’t exist physically.
Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Business Studies: Engaging Questions & Answers for Success

Trending doubts
Which are the Top 10 Largest Countries of the World?

What are the major means of transport Explain each class 12 social science CBSE

Draw a labelled sketch of the human eye class 12 physics CBSE

Why cannot DNA pass through cell membranes class 12 biology CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

Draw a neat and well labeled diagram of TS of ovary class 12 biology CBSE




