Question

Solve in positive integers : $5x+2y=53$
(a) $x=1,3,5,7,9;y=24,19,14,9,4$
(b) $x=2,4,6,8,10;y=23,20,13,8,3$
(c) $x=11,13,15,17,19;y=1,3,4,6,9$
(d) None of these

Answer 1

Hint: In these types of questions , choice by elimination is the best approach . Instead of finding the correct option , we will eliminate the wrong answers and the last option remaining is the correct option.

Complete step by step answer:
To solve this question , we must know the following properties of natural numbers :
Product of two odd numbers is always odd.
Sum of two odd numbers is always even.
Sum of two even numbers is always even.
Sum of an odd and an even number is always odd.
Product of an ever or odd number with an even number is always even.
Now , from the question , we can see that the sum in the RHS is an odd number. So , among the two numbers in the LHS , one is even and the other is odd.
Now , the coefficient of $y$ is an even number. So , the value of $2y$ will always be even . It means the value of $5x$ should be odd. Now , we know , product of two odd numbers is always odd and the product of an odd number and an even number is always even . So, the values of $x$ cannot be even. Hence , option(b) is ruled out.
Now , in option (c) , we can see that the first ordered pair is $(11,1)$, i.e. $x=11$ and $y=1$ . On substituting in $5x+2y$ , we get the value of $5x+2y$ as $(5\times 11)+(2\times 1)=57$ , which clearly is not equal to $53$ . So , option (c) is also ruled out.
Now , in option (a) , the first values are $x=1$ and $y=24$ .
On substituting in $5x+2y$ , we get the value of $5x+2y$ as $(5\times 1)+(2\times 24)=5+48=53$.
So , the first ordered pair of option(a) satisfies the equation.
Now , let’s consider the equation $ax+by=c$. Here, the coefficients of $x$ and $y$ are in the ratio $b:a$. Let $({{x}_{1}},{{y}_{1}})$ satisfy the equation of line. So, $a{{x}_{1}}+b{{y}_{1}}=c$. Let’s consider the points $({{x}_{1}}+b,{{y}_{1}}-a)$. On substituting this point in the equation of line , the LHS becomes $a({{x}_{1}}+b)+b({{y}_{1}}-a)$.
$=a{{x}_{1}}+ab+b{{y}_{1}}-ab$
$=a{{x}_{1}}+b{{y}_{1}}$
$=c$ , which is the same as the RHS of the equation of the line.
Hence, the point $({{x}_{1}}+b,{{y}_{1}}-a)$ will also satisfy the equation of the line, or simply we can say that the point $({{x}_{1}}+b,{{y}_{1}}-a)$ will also lie on the line $ax+by=c$.
Now , we can see that the coefficients of $x$ and $y$ are in the ratio $5:2$ . So , if $(a,b)$ satisfies the equation, then $(a+2,b-5)$ will also satisfy the equation.
Now, $(1,24)$ satisfies the equation . So , $(3,19),(5,14),(7,9)$ and $(9,4)$ will also satisfy the equation.
Hence , option(a) is the correct answer.

Note: The question can also be solved graphically. The equation $5x+2y=53$represents a line , which can be shown in a cartesian plane as

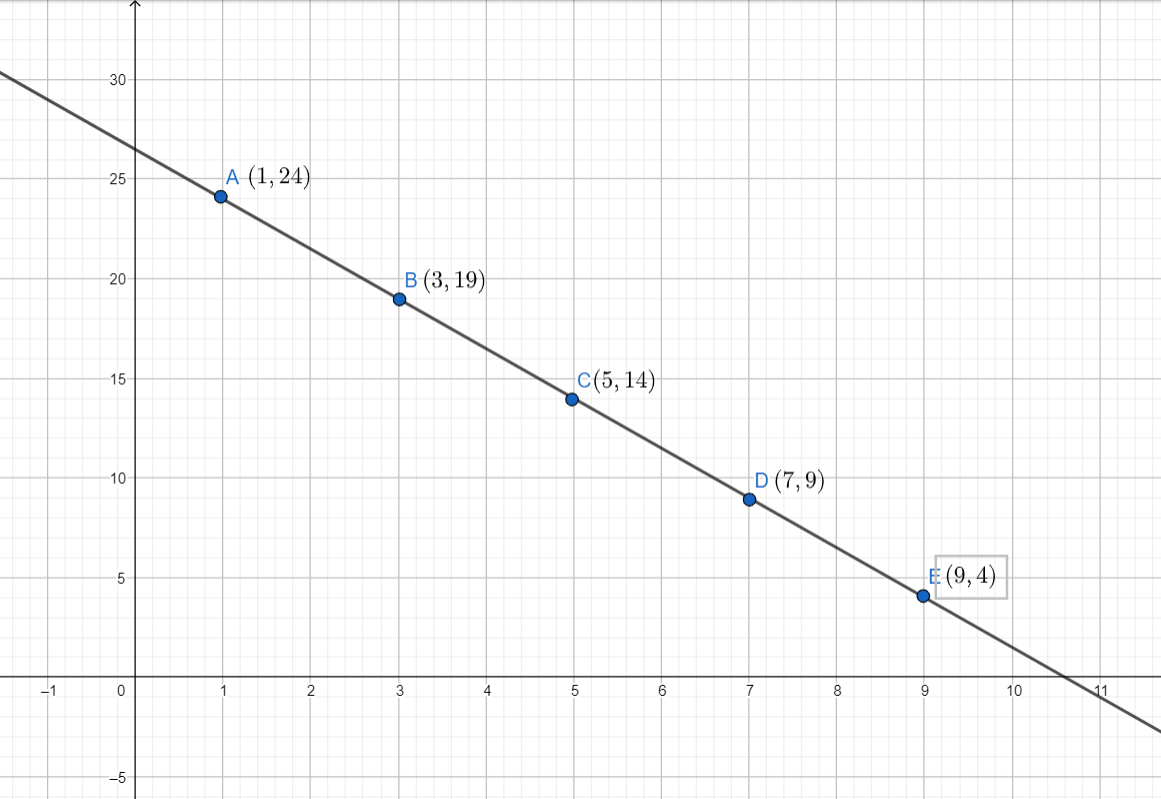
From the graph , we can clearly see that the points $(1,24),(3,19),(5,14),(7,9)$ and $(9,4)$lie on the line $5x+2y=53$.
Hence , option(a) is the correct option .