Question

How do you solve $ - 3x - 2y = 0$ and $3x - y = 18$ by graphing?

Answer 1

Hint: A line can be entirely determined by two points. So, to draw the line just take two points that satisfy the line equation and draw a line through those points in the graph. Plot these lines on the same graph and find the coordinates of their point of intersection. This will give the solution to the given system of equations.

Complete step-by-step solution:
We have, two lines of equations,
$ \Rightarrow - 3x - 2y = 0$...............….. (1)
$ \Rightarrow 3x - y = 18$.............….. (2)
Now, we have to plot given equations on a graph; for this, we require at least two points that lie on that line.
So, consider equation (1),
$ \Rightarrow - 3x - 2y = 0$
Now, substitute $x = 0$,
$ \Rightarrow - 3 \times 0 - 2y = 0$
Simplify the terms,
$ \Rightarrow - 2y = 0$
Divide both sides by -2,
$ \Rightarrow y = 0$
Therefore, (0,0) lies on the above line $ - 3x - 2y = 0$.
Now, substitute $x = 2$,
$ \Rightarrow - 3 \times 2 - 2y = 0$
Simplify the terms,
$ \Rightarrow - 6 - 2y = 0$
Move -6 on the other side,
$ \Rightarrow - 2y = 6$
Divide both sides by -2,
$ \Rightarrow y = - 3$
Therefore, (2,3) lies on the above line $ - 3x - 2y = 0$.
So, consider equation (2),
$ \Rightarrow 3x - y = 18$
Now, substitute $x = 0$,
$ \Rightarrow 3 \times 0 - y = 18$
Simplify the terms,
$ \Rightarrow - y = 18$
Multiply both sides by -1,
$ \Rightarrow y = - 18$
Therefore, (0,-18) lies on the above line $3x - y = 18$.
Now, substitute $y = 0$,
$ \Rightarrow 3x - 0 = 18$
Simplify the terms,
$ \Rightarrow 3x = 18$
Divide both sides by 3,
$ \Rightarrow x = 6$
Therefore, (6,0) lies on the above line $3x - y = 18$.
Now, plot given lines on a graph using obtained points.

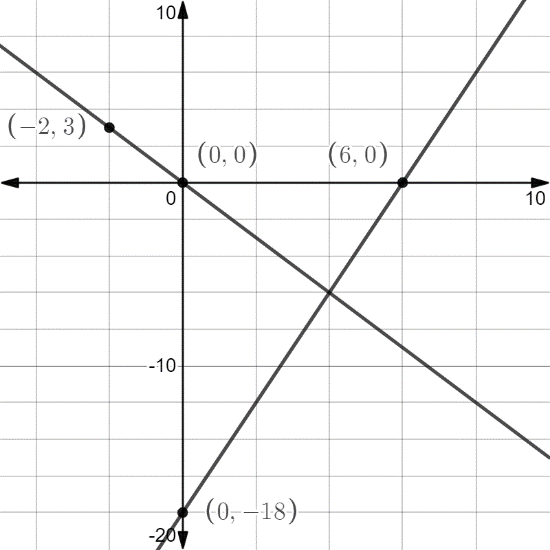
Hence, from the graph, we can see that \[x = 4\] and \[y = - 6\] is the solution of the given system of equations.

Note: Whenever you get this type of question the key concept to solve this is to learn the concept of a system of linear equations containing two equations. The solution of such a system is the ordered pair that is a solution to both the equations of the system. Graphically, the solution is the intersection point where both lines of the system intersect.