
How do you solve $1+\cos x-2{{\sin }^{2}}x=0$ and find all solutions in the interval $0\le x<360$ ?
Answer
555k+ views
Hint: We are given a trigonometric equation in two trigonometric functions, sine and cosine function. In order to simplify this equation, we must apply basic trigonometric identities wahich have been derived and proven by application on the Pythagorean triangle. Then, we shall find solutions for the equation thus obtained in the specific given interval of x.
Complete step-by-step solution:
By the basic properties of trigonometric functions, we know that ${{\sin }^{2}}x+{{\cos }^{2}}x=1$.
Transposing the term ${{\cos }^{2}}x$ to the right-hand side, we get the value of ${{\sin }^{2}}x$ as $1-{{\cos }^{2}}x$ for substitution in the given equation, $1+\cos x-2{{\sin }^{2}}x=0$.
We get, $1+\cos x-2\left( 1-{{\cos }^{2}}x \right)=0$
Simplifying further, we get
$\begin{align}
& \Rightarrow 1+\cos x-2+2{{\cos }^{2}}x=0 \\
& \Rightarrow 2{{\cos }^{2}}x+\cos x-1=0 \\
\end{align}$
Let $\cos x=t$ and putting in our equation, we get
$\Rightarrow 2{{t}^{2}}+t-1=0$
We will now factorize this equation to find the value of t.
$\begin{align}
& \Rightarrow 2{{t}^{2}}+2t-t-1=0 \\
& \Rightarrow 2t\left( t+1 \right)-1\left( t+1 \right)=0 \\
& \Rightarrow \left( t+1 \right)\left( 2t-1 \right)=0 \\
\end{align}$
$\Rightarrow t+1=0$ or $2t-1=0$
$\Rightarrow t=-1$ or $t=\dfrac{1}{2}$
Thus, $t=-1,\dfrac{1}{2}$
Therefore, $\cos x=-1,\dfrac{1}{2}$.
For these two values of x, we shall find the values of x which will satisfy our given range of x with the help of a graph of the cosine of x.
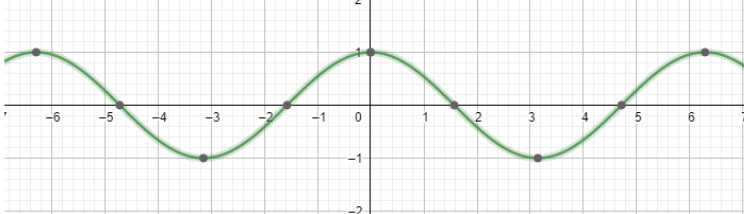
For $\cos x=-1$,
In $0\le x<360$, $\cos x=-1$ at $x=180$.
For $\cos x=\dfrac{1}{2}$,
In $0\le x<360$, $\cos x=\dfrac{1}{2}$ at $x=60,180+60$, that is, at $x=60,\text{ }240$.
Therefore, for $1+\cos x-2{{\sin }^{2}}x=0$ all solutions in the interval $0\le x<360$ are $x=$ 60, 180 and 240.
Note: While simplifying any trigonometric equation, we must always try to simplify them as the sine or cosine functions. This is because only these two functions are the most basic of all the trigonometric functions as they have been derived straight from the Pythagorean theory. Also, we must remember the graphs of the six trigonometric functions to quickly find their solutions in between any interval as given in the question.
Complete step-by-step solution:
By the basic properties of trigonometric functions, we know that ${{\sin }^{2}}x+{{\cos }^{2}}x=1$.
Transposing the term ${{\cos }^{2}}x$ to the right-hand side, we get the value of ${{\sin }^{2}}x$ as $1-{{\cos }^{2}}x$ for substitution in the given equation, $1+\cos x-2{{\sin }^{2}}x=0$.
We get, $1+\cos x-2\left( 1-{{\cos }^{2}}x \right)=0$
Simplifying further, we get
$\begin{align}
& \Rightarrow 1+\cos x-2+2{{\cos }^{2}}x=0 \\
& \Rightarrow 2{{\cos }^{2}}x+\cos x-1=0 \\
\end{align}$
Let $\cos x=t$ and putting in our equation, we get
$\Rightarrow 2{{t}^{2}}+t-1=0$
We will now factorize this equation to find the value of t.
$\begin{align}
& \Rightarrow 2{{t}^{2}}+2t-t-1=0 \\
& \Rightarrow 2t\left( t+1 \right)-1\left( t+1 \right)=0 \\
& \Rightarrow \left( t+1 \right)\left( 2t-1 \right)=0 \\
\end{align}$
$\Rightarrow t+1=0$ or $2t-1=0$
$\Rightarrow t=-1$ or $t=\dfrac{1}{2}$
Thus, $t=-1,\dfrac{1}{2}$
Therefore, $\cos x=-1,\dfrac{1}{2}$.
For these two values of x, we shall find the values of x which will satisfy our given range of x with the help of a graph of the cosine of x.

For $\cos x=-1$,
In $0\le x<360$, $\cos x=-1$ at $x=180$.
For $\cos x=\dfrac{1}{2}$,
In $0\le x<360$, $\cos x=\dfrac{1}{2}$ at $x=60,180+60$, that is, at $x=60,\text{ }240$.
Therefore, for $1+\cos x-2{{\sin }^{2}}x=0$ all solutions in the interval $0\le x<360$ are $x=$ 60, 180 and 240.
Note: While simplifying any trigonometric equation, we must always try to simplify them as the sine or cosine functions. This is because only these two functions are the most basic of all the trigonometric functions as they have been derived straight from the Pythagorean theory. Also, we must remember the graphs of the six trigonometric functions to quickly find their solutions in between any interval as given in the question.
Recently Updated Pages
Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Master Class 11 Physics: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Class 11 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

What organs are located on the left side of your body class 11 biology CBSE

Why is 1 molar aqueous solution more concentrated than class 11 chemistry CBSE

SiO2GeO2 SnOand PbOare respectively A acidic amphoteric class 11 chemistry CBSE

Bond order ofO2 O2+ O2 and O22 is in order A O2 langle class 11 chemistry CBSE

What is 1s 2s 2p 3s 3p class 11 chemistry CBSE




