Question

Slopes of tangents through $A\left( 7,1 \right)$ to the circle $C:{{x}^{2}}+{{y}^{2}}=25$ satisfy the equation
A. $12{{m}^{2}}+7m+12=0$
B. \[12{{m}^{2}}-7m+12=0\]
C. $12{{m}^{2}}+7m-12=0$
D. \[12{{m}^{2}}-7m-12=0\]

Answer 1

Hint: To solve this question, we should know the relation between the tangent of the circle and the circle itself. The perpendicular distance between the centre of the circle and the tangent of the circle is equal to radius of the circle. We are given a point $A\left( 7,1 \right)$ through which tangents are drawn to the circle. By assuming a slope of m, we can write the general equation of the line that passes through $A\left( 7,1 \right)$. The equation of a line with slope m and passing through point $\left( {{x}_{1}},{{y}_{1}} \right)$ is given by $y-{{y}_{1}}=m\left( x-{{x}_{1}} \right)$. The perpendicular distance between a line $ax+by+c=0$ and a point $\left( {{x}_{1}},{{y}_{1}} \right)$ is given by $\text{distance}=\dfrac{\left| a{{x}_{1}}+b{{y}_{1}}+c \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}}}$. Using the distance formula with distance = 5 units(radius) and the point $O\left( 0,0 \right)$ with the derived equation of tangent, we get the required equation containing roots as the slopes of tangents.

Complete step-by-step answer:

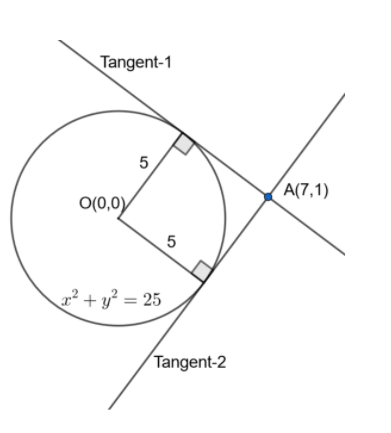
Let us assume the required slope of tangent as m. It passes through the point $A\left( 7,1 \right)$.
The equation of a line with slope m and passing through point $\left( {{x}_{1}},{{y}_{1}} \right)$ is given by $y-{{y}_{1}}=m\left( x-{{x}_{1}} \right)$.
Using this formula, we get the equation of the tangent as
$\begin{align}
  & y-1=m\left( x-7 \right) \\
 & y-1=mx-7m \\
 & mx-y-7m+1=0 \\
\end{align}$
We know the property of a circle that the perpendicular distance between the centre of the circle and the tangent of the circle is equal to radius of the circle.
The perpendicular distance between a line $ax+by+c=0$ and a point $\left( {{x}_{1}},{{y}_{1}} \right)$ is given by $\text{distance}=\dfrac{\left| a{{x}_{1}}+b{{y}_{1}}+c \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}}}$.
The centre and radius of the circle ${{x}^{2}}+{{y}^{2}}={{r}^{2}}$ is $\left( 0,0 \right)$ and r units respectively.
The centre of the given circle $C:{{x}^{2}}+{{y}^{2}}=25$ is $O\left( 0,0 \right)$.
Radius of the given circle is 5 units.
From the distance formula, we can write that
Distance = Radius = 5 units
$\left( {{x}_{1}},{{y}_{1}} \right)=O\left( 0,0 \right)$
The line $ax+by+c=0$ is the equation of tangent $mx-y-7m+1=0$
Using them, we get
$\begin{align}
  & \dfrac{\left| m\times 0-0-7m+1 \right|}{\sqrt{{{m}^{2}}+{{\left( -1 \right)}^{2}}}}=5 \\
 & \left| 1-7m \right|=5\times \sqrt{{{m}^{2}}+1} \\
\end{align}$
Squaring on both sides, we get
$\begin{align}
  & {{\left( \left| 1-7m \right| \right)}^{2}}={{\left( 5\times \sqrt{{{m}^{2}}+1} \right)}^{2}} \\
 & 49{{m}^{2}}-14m+1=25\left( 1+{{m}^{2}} \right) \\
 & 49{{m}^{2}}-14m+1=25+25{{m}^{2}} \\
 & 24{{m}^{2}}-14m-24=0 \\
\end{align}$
Dividing by 2 we get
$12{{m}^{2}}-7m-12=0$
$\therefore $ The slopes of the tangent from $A\left( 7,1 \right)$ satisfy the equation $12{{m}^{2}}-7m-12=0$. The answer is option-D

Note: An alternative way to do the problem is by writing the general equation of the tangent of the circle. The general equation of a tangent of the circle ${{x}^{2}}+{{y}^{2}}={{r}^{2}}$ is given by $y=mx\pm r\sqrt{1+{{m}^{2}}}$. The general equation of the tangent of ${{x}^{2}}+{{y}^{2}}=25$ is
$y=mx\pm 5\sqrt{1+{{m}^{2}}}$. As the tangent passes through $A\left( 7,1 \right)$, the point should satisfy the equation of the tangent $y=mx\pm 5\sqrt{1+{{m}^{2}}}$. We can write that
$\begin{align}
  & 1=7m\pm 5\sqrt{1+{{m}^{2}}} \\
 & 1-7m=\pm 5\sqrt{1+{{m}^{2}}} \\
\end{align}$
Squaring on both sides gives the required result.