Question

Sketch the graphs of the curves $ {{\text{y}}^2} = {\text{x}} $ and $ {{\text{y}}^2} = 4 - 3{\text{x}} $ , and find the area enclosed between them.

Answer 1

Hint: To find the area enclosed between the curves, we find the vertex of the parabola formed and find their points of intersection. Then we look at the figure and integrate the respective curve equations w.r.t their limits to compute the area.

Complete step-by-step answer:
We sketch an appropriate graph of both the equations.
The graph of the equations can be determined by substituting random values of x, solving for y. We plot all such points on the graph and join them.

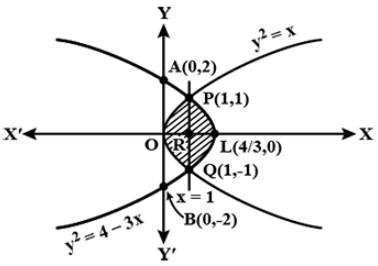
The points of intersection of both the curves are obtained by solving their equations.
 $ {{\text{y}}^2} = {\text{x}} $ and $ {{\text{y}}^2} = 4 - 3{\text{x}} $ .
Hence x = 4 – 3x
⟹4x = 4
⟹x = 1
Hence $ {{\text{y}}^2} = {\text{ 1}} $ ⟹y = ±1.
Hence their points of intersection are (1, 1) and (1, -1), let these points be P and Q respectively. Also PQ cuts the x – axis at point R.
For an equation of the parabola of the form $ {{\text{y}}^2} = {\text{a}}\left( {{\text{x - h}}} \right) + {\text{k}} $ , the vertex is given by (h, k).
Consider the given equation $ {{\text{y}}^2} = 4 - 3{\text{x}} $ ⟹ $ {{\text{y}}^2} = {\text{ - 3x + 4 = - 3}}\left( {{\text{x - }}\dfrac{4}{3}} \right) $ .
Hence the vertex L of this parabola is $ \left( {\dfrac{4}{3},0} \right) $ . It cuts the y – axis at A (0, 2) and B (0, -2).
As we now know the points at which these curves cut the x and y axis. The enclosed area is the shaded part of the figure.
Now according to the figure, the total enclosed area is POQLP.
∴Total area of POQLP = 2 times the area of OPLRO
Now observing the shaded part OPLRO from the figure carefully, we could say that it comprises both the curves equally. Hence we integrate the curve equation $ {{\text{y}}^2} = {\text{x}} $ from the limits 0 to 1 for x and add it to the result of the integral of the curve equation $ {{\text{y}}^2} = 4 - 3{\text{x}} $ with limits of x from 1 to $ \dfrac{4}{3} $ .
Hence the total area of POQLP = 2 $ \left[ {\int\limits_0^1 {\sqrt {\text{x}} {\text{dx}}} + \int\limits_1^{\dfrac{4}{3}} {\sqrt {{\text{4 - 3x}}} {\text{dx}}} } \right] $
 $
   \Rightarrow 2\left[ {\left( {\dfrac{{{{\text{x}}^{\dfrac{3}{2}}}}}{{\dfrac{3}{2}}}} \right)_0^1 + \left( {\dfrac{{2{{\left( {{\text{4 - 3x}}} \right)}^{\dfrac{3}{2}}}}}{{ - 3 \times 3}}} \right)_1^{\dfrac{4}{3}}} \right] \\
   \Rightarrow 2\left[ {\left( {\dfrac{{{1^{\dfrac{3}{2}}}}}{{\dfrac{3}{2}}} - \dfrac{{{0^{\dfrac{3}{2}}}}}{{\dfrac{3}{2}}}} \right) + \left( {\dfrac{{2{{\left( {{\text{4 - 3}}\left( {\dfrac{4}{3}} \right)} \right)}^{\dfrac{3}{2}}}}}{{ - 3 \times 3}} - \dfrac{{2{{\left( {{\text{4 - 3}}\left( 0 \right)} \right)}^{\dfrac{3}{2}}}}}{{ - 3 \times 3}}} \right)} \right] \\
   \Rightarrow 2\left[ {\left( {\dfrac{2}{3} - 0} \right) - \dfrac{2}{9}\left( {0 - 1} \right)} \right] \\
   \Rightarrow 2\left[ {\dfrac{2}{3} + \dfrac{2}{9}} \right] \\
   \Rightarrow 2\left[ {\dfrac{{6 + 2}}{9}} \right] = \dfrac{{16}}{9}{\text{ sq units}} \\
        $ :-- $ \left( {\int {\sqrt {\text{x}} {\text{dx = }}\int {{{\text{x}}^{\dfrac{1}{2}}}{\text{dx = }}\dfrac{{{{\text{x}}^{\dfrac{1}{2} + 1}}}}{{\dfrac{1}{2} + 1}}{\text{ }}\left( {{\text{i}}{\text{.e}}{\text{. }}\dfrac{{{{\text{x}}^{{\text{n + 1}}}}}}{{{\text{n + 1}}}}} \right)} } } \right) $
Hence the area enclosed between the curves is $ \dfrac{{16}}{9} $ sq units.

Note – In order to solve questions of this type the key is to know the method of applying integration to the equations. It is tricky to figure out the limits of integrals of both equations. We need to make use of a precisely drawn figure and label it accordingly to help us with the solution. The formulae of integrals of general functions is necessary.