Question

Sketch the graph for $y={{\sec }^{-1}}\sec x$.

Answer 1

Hint: In this question, we will first write secant function in terms of cos then understand the relation of $\cos x$ and ${{\cos }^{-1}}x$. We will observe the graph of $\cos x$ , and how they change signs and use it to plot a graph of $y={{\sec }^{-1}}\sec x$.
Complete step-by-step answer:
In given question, we have,
$y={{\sec }^{-1}}\sec x$
This can be written as
$\sec y=\sec x$.
We know that $\sec x=\dfrac{1}{\cos x}$, therefore, we can write above equation as,
$\dfrac{1}{\cos y}=\dfrac{1}{\cos x}$
Cross multiplying this, we get,
$\cos x=\cos y$
This can be written as,
$y={{\cos }^{-1}}\cos x$.
So, the graph of $y={{\sec }^{-1}}\sec x$ is the same as the graph of $y={{\cos }^{-1}}\cos x$.
Now, $\cos x$ is a periodic function with period $2\pi $, which means its values repeat in the same pattern after $2\pi $ increases in $x$. That is, $\cos x=\cos \left( 2\pi +x \right)$.
Since, cos x is periodic with period $2\pi $. Therefore, $y={{\cos }^{-1}}\cos x$ is also period with period $2\pi $.
Also, the domain here is a set of those values of $x$ for which ${{\cos }^{-1}}\cos x$ is defined. And, range is the set of values where ${{\cos }^{-1}}\cos x$ lies.
Now, for all real values of $x$, $\cos x$ lies between -1 and 1. And, between -1 and 1, the inverse function of cosine is defined. Therefore, ${{\cos }^{-1}}\cos x$ is defined for all real values of$x$.
We know, graph of $y=\cos x$ is:

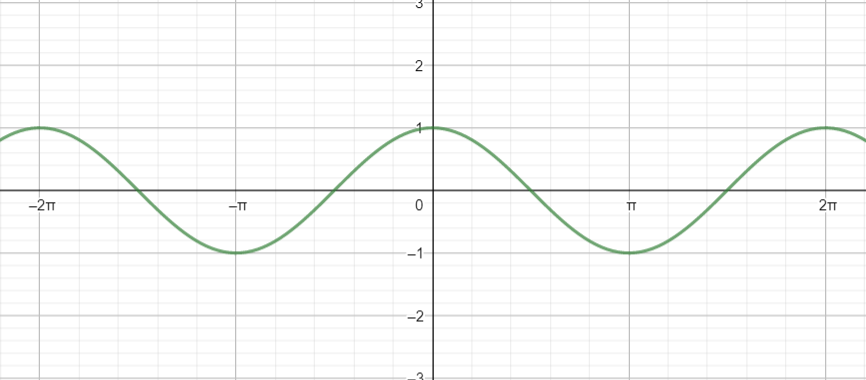
We see that, in the interval $\left[ -\pi ,\pi \right]$ , for two different values of $x$ , we have the same value of $y$.
Also, from definition of cosine inverse, in this graph, we get,
${{\cos }^{-1}}y=x$
If we substitute $y=\cos x$ here, we get,
${{\cos }^{-1}}\cos x=x$.
Now, in graph of ${{\cos }^{-1}}\cos x$, we have,
 $y={{\cos }^{-1}}\cos x$
$\Rightarrow y=x$
But, in the interval $\left[ -\pi ,\pi \right]$ , for two different values of $x$ , we have the same value of $y$ .
Let those two different values be represented by ${{y}_{1}},{{y}_{2}}$.
Now, as $x$ increases from $-\pi $ to 0, $\cos x$ increases from -1 to 1, and hence, ${{\cos }^{-1}}\cos x$ decreases from $\pi $ to 0. Therefore, here we will have, ${{y}_{1}}=-x$.
And as it increases from 0 to $\pi $, $\cos x$ decreases from 1 to -1, and hence, ${{\cos }^{-1}}\cos x$ increases from 0 to $\pi $. Therefore, here we will have, ${{y}_{2}}=x$ .
Also, from $-\pi $ to$\pi $, the length of interval is $2\pi $ and ${{\cos }^{-1}}\cos x$ periodic with period $2\pi $. Therefore, the rest of the graph will repeat the same as in interval $\left[ -\pi ,\pi \right]$.
Hence, the graph of ${{\cos }^{-1}}\cos x$ is given by:

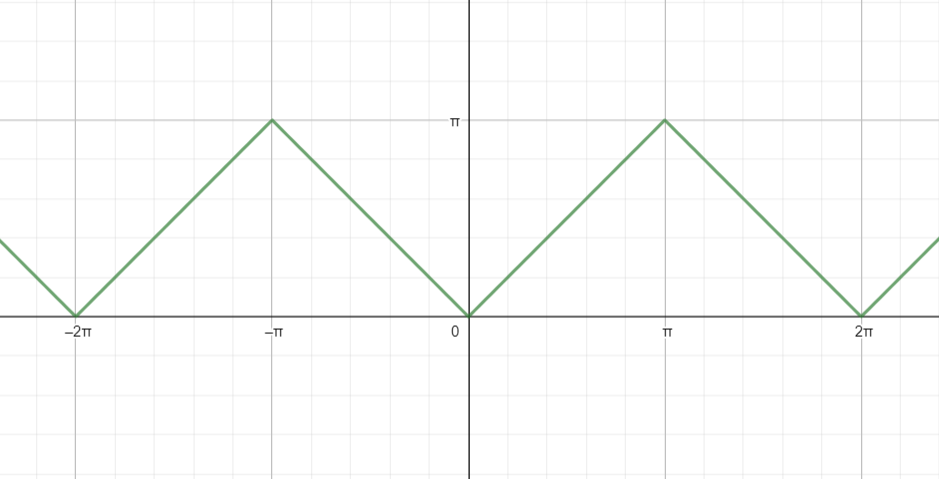
Hence for the graph of $y={{\sec }^{-1}}\sec x$ is plotted above.

Note: While plotting the graph, keep in mind that for two different values of $x$ , ${{\cos }^{-1}}\cos x$ will have the same value in interval of length $2\pi $. So, looking at $y=x$, do not directly plot a graph of an infinite straight line.