Question

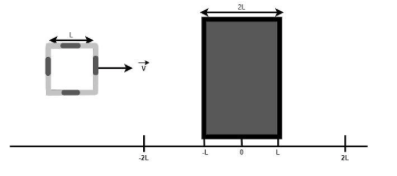
Sketch a graph of the induced current in the loop as a function of x. Take counter clockwise currents to be positive.

Answer 1

Hint:The loop when entering the magnetic field will induce electric current in the loop and the loop while exiting the magnetic field will induce an current but when the loop (not moving) is inside the magnetic field and the magnetic field is uniform (assumption taken) there would be no current will induced in the coil.

Complete step by solution:
According to Faraday's law of electromagnetic induction the magnitude of the induced emf is directly proportional to the rate of change of magnetic flux.
$\varepsilon = \dfrac{{d\phi }}{{dt}}$ ;
Where:
$\varepsilon $= Electromotive force;
$\phi $= Magnetic flux;
t = time;
Now, flux is given as:
$\phi = Blx$;
Where:
 $\phi $= Magnetic flux.
B = Magnetic Field;
l = Length;
x = Distance;
Put the value of flux in the equation$\varepsilon = \dfrac{{d\phi }}{{dt}}$:
$\varepsilon = \dfrac{{d\left( {Blx} \right)}}{{dt}}$;
$ \Rightarrow \varepsilon = \dfrac{{d\left( x \right)}}{{dt}}lB$;
Now, we know that the velocity ‘v’ is the change in distance with respect to time (dx/dt):
$ \Rightarrow \varepsilon = Blvd$; ….$\left( {\dfrac{{d\left( x \right)}}{{dt}} = v} \right)$;
Now, the force on a wire in a uniform magnetic field is given by:
$F = ilB$;
Where:
i = Current;
F = Force;
l = Length;
B = Magnetic Field;
Now, According to ohm’s Law:
$v = ir$;
Where:
v = Voltage Source;
i = Current;
r = Resistance;
Now, here the EMF “$\varepsilon $” is acting as a voltage source so,
$\varepsilon = ir$;
In terms of current:
$ \Rightarrow i = \dfrac{\varepsilon }{r}$;
Now, put the above relation in the equation$F = ilB$:
$F = \left( {\dfrac{\varepsilon }{r}} \right)lB$;
Now, put the value of emf $\varepsilon = - Blv$in the above equation:
\[F = \left( {\dfrac{{Blv}}{r}} \right)lB\];
\[ \Rightarrow F = \left( {\dfrac{{{B^2}{l^2}v}}{r}} \right);\]

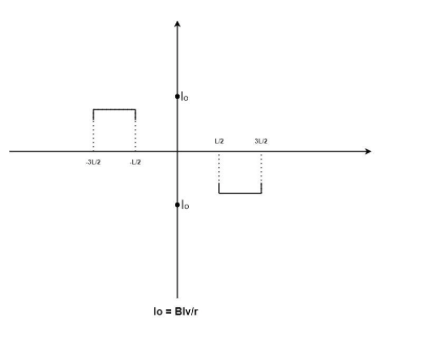
If the loop enters the magnetic field the magnetic force will induce electric current in the direction which is opposite to the direction of the magnetic field. Suppose, the magnetic field is inside \[\left( \otimes \right)\] the area then if the loop is entering the magnetic field then the direction of the induced current will be outside $\left( \bullet \right)$ the area and when the current carrying loop is exiting the magnetic field then the induced current would be inside \[\left( \otimes \right)\] the area.

Magnetic force will always remain positive.

Note:Here, we need to apply Faraday’s law, ohm’s law and lenz law and explain about the nature of the induced current in the coil due to the magnetic field. Here, the magnetic force will act only two times: one when the coil is entering the magnetic field and second when the coil is exiting the magnetic field.